L'Imagerie par Résonance Magnétique (IRM) a été développée à partir de 1973. Elle est rapidement devenue la méthode de choix dans plusieurs domaines médicaux, en particulier ceux en relation avec le cerveau (étude des maladies neurologiques, visualisation du cerveau en activité...). L'IRM est adaptée d'une des principales techniques d'analyse utilisée en chimie, la Résonance Magnétique Nucléaire (RMN). Cet article expose le principe physique commun aux deux méthodes.
Interaction noyau - champ magnétique
L'IRM et la RMN ont pour base le même effet physique : la possibilité pour certains noyaux atomiques d'interagir avec un champ magnétique. Pour que cette interaction soit observée, le noyau doit avoir un spin nucléaire non-nul. Le spin nucléaire est une caractéristique quantique intrinsèque du noyau comme sa masse et sa charge, il peut prendre des valeurs entières ou demi-entières : 0, 1/2, 1 et 3/2 pour les noyaux les plus courants (cf tableau 1.) On remarque que les isotopes[1]d'un élément peuvent avoir des spins différents.
|
Spin nucléaire |
0 (ces noyaux sont inactifs en IRM et RMN) |
1/2 |
1 |
3/2 |
|
Noyau |
12C, 16O |
1H, 13C, 15N, 19F, 31P |
2H (deutérium), 14N |
11B, 23Na, 35Cl, 37Cl |
En présence d'un champ magnétique B0, le spin nucléaire donne naissance à un moment magnétique de spin μ dont l'amplitude est proportionnelle à la valeur du spin. Cet effet n'est donc observable que si le spin est non nul, les noyaux de spin nul sont inexploitables en RMN et IRM. Le moment μ est animé d'un mouvement de précession autour de l'axe de B0, tel une toupie autour de la verticale, avec une pulsation propre ω0 proportionnelle à l'intensité B0 (figure 1.)
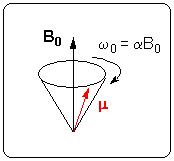
Figure 1. Mouvement de précession du moment magnétique de spin autour d'un champ magnétique.
Voyons à présent comment la RMN tire profit de ce mouvement pour analyser la structure de la matière.
Principe de la RMN
Le principe de la mesure de résonance magnétique nucléaire est de mettre le moment μ en mouvement de précession autour d'un champ B0 puis de perturber ce mouvement à l'aide d'un deuxième champ magnétique B1 appliqué pendant un court instant. Cela dévie la trajectoire de μ, mais une fois B1 disparu, il retrouve son mouvement initial en présence de B0 seul. Ce retour à l'équilibre s'accompagne d'une émission d'ondes électromagnétiques que l'on peut détecter : c'est le signal mesuré en RMN et IRM.
Examinons plus en détail ce qui ce passe pendant une expérience de RMN. Pour cela considérons un ensemble de spins nucléaires non-nuls, par exemple les spins d'un groupe de proton, noyau de l'hydrogène, de spin 1/2. C'est le noyau le plus utilisé en RMN comme en IRM.
-
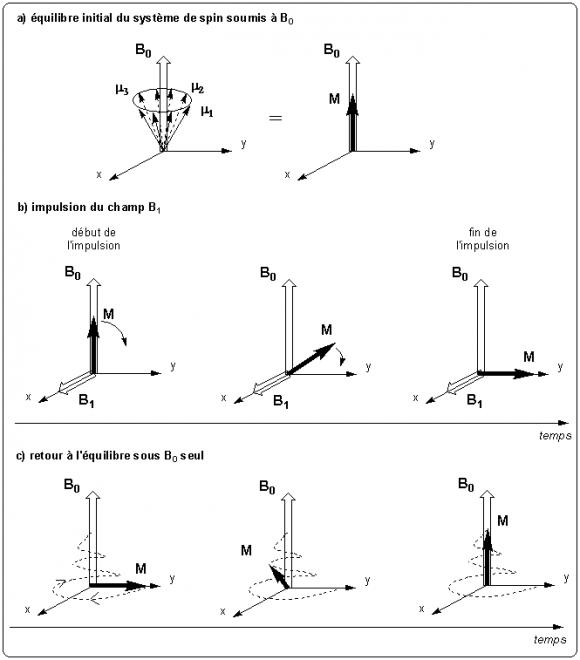
On applique un champ magnétique statique B0 tous les moments μ précessent autour de l'axe de B0 avec une pulsation propre μ0. La résultante de l'ensemble des moments est une aimantation M alignée suivant B0 (figure 2a). On s'intéresse maintenant à cette aimantation résultante M.
-
On applique ensuite un champ B1 dans une direction perpendiculaire à B0. Ce champ n'est pas uniforme mais alternatif de fréquence égale à la fréquence de précession des moments μ autour de B0 que l'on appelle la fréquence de résonance. Les moments magnétiques subissent maintenant l'action de la résultante B0 + B1 qui a pour effet de déplacer M autour de l'axe de B1 (figure 2b).
-
Une fois que M a basculé dans le plan perpendiculaire à B0, on coupe le champ B1. Le système est alors hors-équilibre et l'aimantation M tend à retrouver sa position initiale en présence de B0 seul. On observe un retour à l'équilibre (figure 2c) qui s'accompagne d'une émission d'onde électromagnétique que l'on peut détecter : c'est le signal de RMN.
Précisons que cette présentation est simplifiée, on peut se reporter à la bibliographie pour avoir l'approche plus rigoureuse (orientation des moments μ, construction de M, mouvement dans le référentiel tournant...) [1-3].
Pour que la séquence précédente puisse se dérouler convenablement, les champs magnétiques mis en jeu doivent présenter les caractéristiques suivantes :
-
B0 doit être très intense. Aujourd'hui, les spectromètres de RMN usuels génèrent un champ entre dix et vingt teslas (de l'ordre de 105 fois le champ magnétique terrestre.) Pour obtenir des champs d'une telle intensité, il faut avoir recours à des bobines supraconductrices refroidies à l'hélium liquide.
-
B1 est un champ radiofréquence alternatif de fréquence égale à la fréquence de précession des moments μ autour de B0 et de faible intensité (de l'ordre de 10-3 T.) Il n'est activé que durant une courte impulsion (de l'ordre de 10 μs.) Il est généré par l'application d'un courant sinusoïdal dans une bobine d'axe perpendiculaire à B0.
Le signal RMN
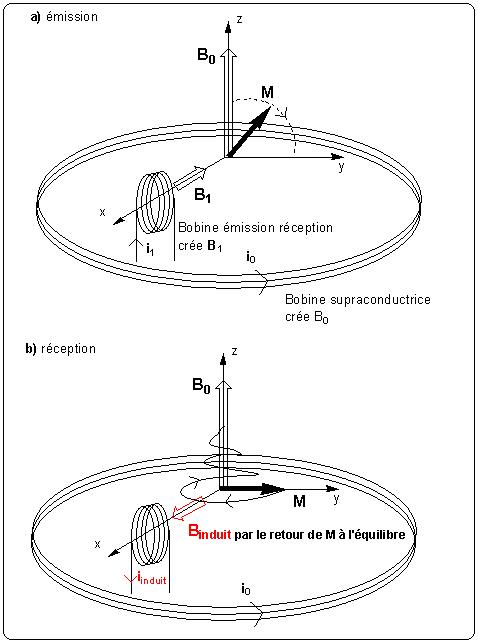
La mesure du signal RMN est étroitement liée au dispositif d'émission de l'impulsion. Le champ B1 est induit par la circulation d'un courant dans une bobine solénoïde (figure 3a.) Lorsque l'on coupe l'impulsion B1 le système de spin retourne à l'équilibre en produisant un champ électromagnétique qui induit un courant dans cette même bobine (figure 3b.) Elle sert donc à la fois de système d'émission et de réception. Ce courant induit est le signal effectivement mesuré.
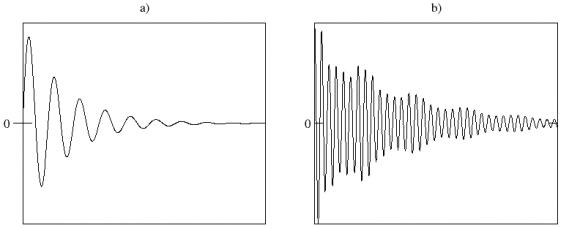
La courbe qui donne le courant induit en fonction du temps est appelée FID pour Free Induction Decay ou « signal de précession libre » en français. Son allure pour un système élémentaire (un proton isolé) est relativement simple : il s'agit d'une sinusoïde amortie exponentiellement (figure 4a.) Mais elle se complique très vite avec le nombre de noyaux mis en jeu : on obtient alors une somme de sinusoïdes amorties de caractéristiques différentes et le FID devient ininterprétable (figure 4b.) Pour pouvoir exploiter la mesure il faut faire appel à une opération mathématique de traitement du signal : la transformée de Fourier.
Traitement du signal par transformée de Fourier
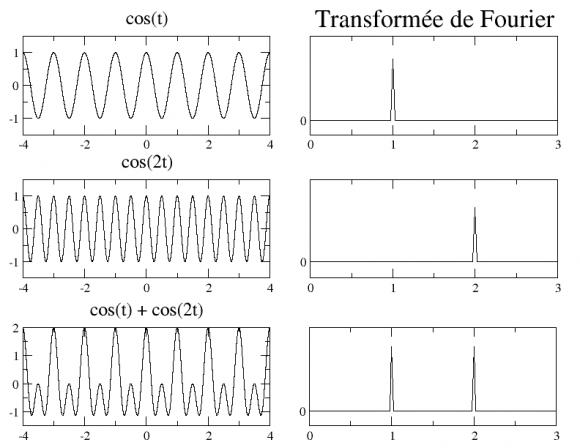
La transformée de Fourier[2] (TF) est une opération mathématique qui permet de déterminer le spectre de fréquence d'un signal temporel f(t) [1-5]. La figure 5 donne la TF de signaux périodiques simples : les fonctions cos(t), cos(2t) et leur somme. On constate que la TF de cos(t) est un pic centré sur 1 et celle de cos(2t) un pic centré sur 2. La TF de la somme cos(t) + cos(2t) fait apparaître deux pics bien séparés centrés sur 1 et 2, on a donc immédiatement les informations sur les fréquences qui composent ce signal. Dans ce cas élémentaire on peut encore trouver cette information en étudiant directement le signal, mais dans le cas d'un signal compliqué comme le FID de la figure 4b la TF devient indispensable.
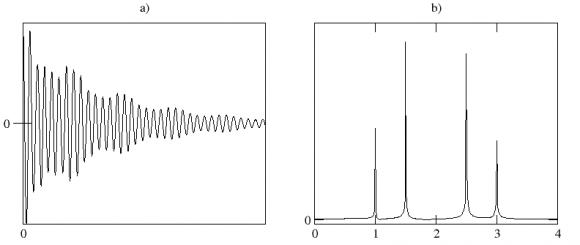
La transformée de Fourier du FID d'un système complexe donne des informations sur les différentes contributions au signal : chaque pic est centré sur la fréquence d'une contribution et sa surface est proportionnelle à l'amplitude de la contribution[3] (figure 6.)
L'analyse chimique par RMN
La transformée de Fourier permet de rendre le signal RMN lisible. Voyons comment on interprète la structure de ce spectre. Pour cela nous raisonnerons sur une molécule simple : l'éthanol CH3CH2OH. La connectivité de chaque atome est donnée sur la formule développée (figure 7.)
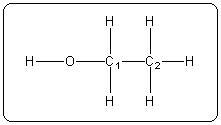
Figure 7. Formule développée de l'éthanol.
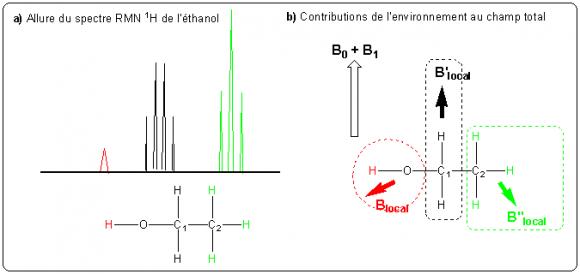
L'éthanol présente six noyaux d'atome d'hydrogène actifs en RMN (par simplification on parle de « proton »). Considérons une molécule d'éthanol de l'échantillon placé dans le spectromètre. Ses six protons sont soumis à des champs B0 et B1 identiques, ils devraient donc présenter la même réponse à l'impulsion B1 et le signal résultant devrait être la somme des six signaux individuels identiques. Le spectre obtenu par transformée de Fourier ne devrait donc faire apparaître qu'un seul pic situé à la fréquence de résonance du proton isolé et de surface six fois celle du pic du proton isolé. Pourtant la structure du spectre est bien plus complexe (figure 8a.) Pour l'interpréter il faut examiner plus en détail le champ magnétique local autour de chaque proton. Il existe des charges en mouvement dans l'entourage immédiat des noyaux, en particulier des électrons. Or les électrons en mouvement induisent des champs magnétiques d'intensité très faible par rapport à B0 (de l'ordre de 10-6 fois plus faible) : ils perturbent faiblement la réponse des noyaux au champ B0 + B1 mais la sensibilité du dispositif de mesure est assez grande pour détecter cette variation.
Il y a dans l'éthanol trois groupes de protons différents, portés respectivement par C1, C2 et O. Chaque proton au sein d'un même groupe est soumis à un champ local identique mais les trois champs locaux sont différents (figure 8b.) Cela entraîne pour chaque groupe une réponse différente à l'impulsion B1, ce qui explique l'existence de trois massifs bien distincts. La sous-structure des massifs est quand à elle due à des phénomènes de couplage entre les spins nucléaires des différents groupes que nous ne détaillerons pas ici (cf bibliographie [1-3].)
Il faut insister sur le fait que même si les variations entre deux signaux sont très faibles, elles permettent d'utiliser la RMN pour l'analyse chimique. À partir des années 1960 elle a été utilisée pour résoudre les structures de molécules organiques relativement petites (de 10 à 100 atomes) puis les progrès techniques et conceptuels ont permis d'élargir considérablement son domaine d'application [6-9]. Les chimistes accèdent aujourd'hui à des processus dynamiques et élucident des structures de plus en plus complexes : protéines, acides nucléiques, polymères...
Une contrainte technique fondamentale : l'homogénéité du champ statique
Considérons maintenant non plus une molécule d'éthanol isolée mais l'échantillon macroscopique réellement utilisé dans l'expérience. La molécule étudiée est en général en solution dans un solvant inactif en RMN. Le volume du tube introduit dans le spectromètre est de l'ordre du mL, donc pour une solution de concentration 10-3 mol/L l'échantillon contient environ 6.1018 molécules. C'est un nombre considérable qui occupe un volume de l'espace bien plus important qu'une seule molécule, il faut vérifier si la situation d'une molécule décrite dans le paragraphe précédent est généralisable à tout l'échantillon.
Supposons que le champ B0 ne soit pas tout à fait le même d'un endroit à l'autre de l'espace de mesure. Alors deux molécules différentes ne sont plus soumises au même champ statique et les protons de groupes identiques ne sont plus soumis au même champ local ce qui engendre un signal différent. Dans le cas extrême d'un champ B0 très inhomogène dans l'échantillon, on observe pour des protons analogues autant de signaux que de zones de champ différentes ce qui interdit toute tentative d'attribution de signaux (figure 9a.)
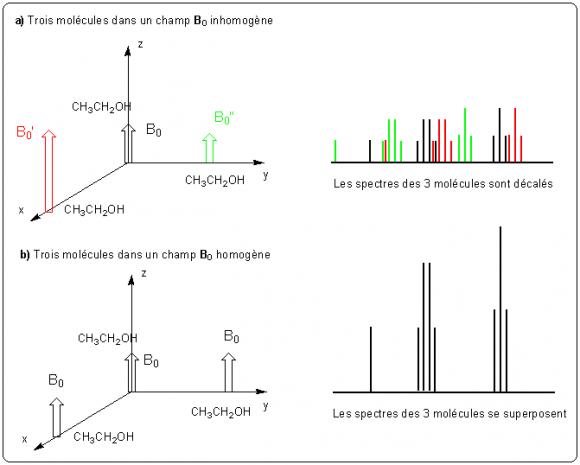
Il faut donc obtenir un champ B0 le plus homogène possible dans tout le volume occupé par l'échantillon si on veut utiliser la RMN comme outil d'analyse structurale. C'est seulement dans ce cas que deux protons analogues sur deux molécules différentes produiront des signaux identiques qui s'additionneront sur le spectre (figure 9b.) On peut évaluer la contrainte sur l'homogénéité : il faut que les variations de B0 soient négligeables devant les variations dues à l'environnement structural des noyaux, donc devant 10-6B0. La technologie actuelle permet d'obtenir des champs homogènes à 10-9 B0 près. Pour cela on utilise des petites bobines correctrices disposées autour de l'échantillon en complément du solénoïde supraconducteur. Elles permettent d'ajuster finement le champ en lui ajoutant des contributions très localisées dans l'espace.
Dans la partie suivante, nous examinons comment les inhomogénéités de champ statique, à proscrire en RMN, sont mises à profit en IRM pour obtenir une information spatiale.
Bibliographie
Ouvrages généraux
[1] « La RMN : Concepts, méthodes et applications », D. Canet, 2ème éd. 2002, Dunod.
[2] « Nuclear Magnetic Resonance », P. J. Hore, 1995, Oxford University Press.
[3] « Chimie physique », P.-W. Atkins, J. de Paula, 2ème éd. 2004, De Boeck.
Histoire de la RMN
[6] « Histoire de la RMN », M. Goldman. Article sur l'évolution de la RMN, de ses débuts aux développements et applications les plus récents, en ligne sur CultureSciences-Chimie
Notes
[1] Les éléments chimiques qui constituent la matière sont tous bâtis sur le même modèle : l'atome est constitué d'un noyau composé de protons, chargés positivement, et de neutrons, électriquement neutres. Autour de ce noyau gravitent des électrons, particules chargées négativement. Le nombre de protons est égal au nombre d'électrons, ce qui assure la neutralité de l'édifice atomique. Ce nombre, caractéristique de l'élément chimique, est le numéro atomique, noté Z. On observe que le nombre de neutron d'un élément peut varier, on parle alors d'isotopes de l'élément chimique. Les isotopes sont caractérisés par le nombre de masse, noté A, égal à la somme du nombre de protons et de neutrons ; on différencie les isotopes d'un élément X par la notation AX. Par exemple, le noyau de l'atome d'hydrogène est constitué d'un proton qui peut, à l'état naturel, être accompagné de zéro, un ou deux neutron(s). L'hydrogène existe donc sous trois formes isotopiques 1H (noté simplement H), 2H (appelé deutérium, noté D) et 3H (appelé tritium, noté T).
[2] Joseph Fourier 1768-1830, mathématicien et physicien français.
[3] Dans le cas d'un pic très fin, sa hauteur est proportionnelle à la contribution en première approximation.
[4] Sur un spectre RMN la surface d'un pic est proportionnelle à la quantité de noyau à l'origine du signal.