Parmi les outils d'analyse disponibles à l'heure actuelle, la RMN est sans doute l'un des plus précieux. Elle a non seulement permis aux chimistes d'identifier beaucoup plus facilement qu'auparavant leurs molécules, ou de caractériser celles extraites de la nature afin d'élaborer de nouveaux médicaments, mais aussi d'obtenir une méthode non-invasive et non-ionisante d'étude du corps humain (Imagerie par Résonance Magnétique, IRM)
Introduction
Nous nous proposons dans ce dossier de poser les bases théoriques de cet outil et d'esquisser son utilisation en chimie en exposant dans un premier temps le magnétisme nucléaire avant de présenter les principaux facteurs utiles aux chimistes pour finir sur une description de l'appareillage utilisé.
Bases théoriques et utilisation en chimie
Certains noyaux se comportent comme de petits aimants, ce qui est le cas de l'hydrogène, du fluor, du phosphore et de bien d'autres. Par ces termes, la notion d'élément1 est sous-entendue , or en RMN, nous nous intéressons aux noyaux, pour éviter la confusion, il nous faut préciser le nombre de masse de façon à les caractériser sans aucune équivoque ; nous parlerons donc de l'hydrogène 1H, du fluor 19F, ou du phosphore 31P. La nuance a son importance puisque au sein d'un même élément, les noyaux peuvent avoir des propriétés tout à fait différentes. Le carbone 12C par exemple ne peut être observé par RMN alors qu'un de ses isotopes2 , le carbone 13C, l'est ; de même, même si les azotes 14N et 15N peuvent tous deux être étudiés par RMN, leur comportement est très différent. L'important pour le chimiste est de savoir que pour chaque élément, il existe au moins un isotope qui soit actif en RMN. Bien entendu, il reste les problèmes de la sensibilité du noyau ainsi que de son abondance qui limitent souvent l'étude de noyaux plus « exotiques » que ceux cités précédemment.
Les noyaux les plus étudiés, dans le cadre de la chimie organique sont l'hydrogène 1H (abondance 99,8 %), le fluor 19F (100 %), le phosphore 31P (100 %) et le carbone 13C (1,1 %)3 et l'azote 15N (0,37 %).
A l'état naturel, ces petits aimants ou spins, sont très peu intenses et caractéristiques du noyau étudié, tout comme leur masse, leur charge, etc. En dehors de toute contrainte extérieure, chaque spin possède une orientation quelconque, le magnétisme résultant est alors nul à notre échelle. Toutefois dès qu'un champ magnétique extérieur est appliqué, ils ont tendance à s'ordonner dans ce champ, produisant un ordre tel qu'une aimantation nucléaire macroscopique peut alors être perçue4 (cette aimantation s'aligne dans la direction du champ, comme l'aiguille d'une boussole dans le champ magnétique terrestre). En apportant de l'énergie au système, sous forme d'ondes électromagnétiques à des fréquences du même ordre de grandeur que celle des ondes radio, il est possible de provoquer une variation de l'aimantation nucléaire qui, bien que très faible, est parfaitement observable et est à la base du phénomène de résonance magnétique nucléaire.
Tel que nous l'avons décrit, tous les noyaux d'un même isotope devraient résonner à la même fréquence. C'est ce qu'avaient prévu les découvreurs de la RMN qui pensaient en faire un outil d'analyse élémentaire, certes plus complexe que les chambres à combustion classiques, mais qui n'apportait d'autre avantage que la possibilité de récupérer le produit après l'expérience.
Malheureusement pour eux, et heureusement pour nous, les noyaux ne sont jamais seuls (du moins dans les conditions qui nous intéressent), les électrons, par leur mouvement, et les noyaux voisins, par leur spin, modifient le champ magnétique vu par le noyau étudié. La variation est très faible (de l'ordre de la partie par million, ppm) mais visible et constitue le déplacement chimique δ d'un noyau dans un environnement donné. Par exemple dans le cas du proton, si un noyau est placé à côté d'un groupe qui a tendance à attirer les électrons, ces derniers auront moins tendance à masquer le champ externe et le noyau résonnera à une fréquence plus élevée5. Des tables permettant d'avoir une idée du déplacement chimique en fonction de l'environnement (et réciproquement) existent.
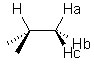
Dans une même molécule, l'influence des autres noyaux magnétiquement actifs sur un noyau observé est aussi un facteur important à prendre en compte : par l'intermédiaire des liaisons chimiques leur spin induit un champ magnétique indépendant du champ extérieur appliqué dont l'influence est loin d'être négligeable, d'autant plus qu'ils sont proches du noyau étudié. Examinons le cas d'un proton situé à côté d'un groupe méthyle CH3 :
Chaque noyau peut se présenter dans deux états différents, soit dans le sens opposé, ainsi, nous obtenons huit configurations différentes :
| Ha | Hb | Hc | Résultante | Multiplicité | Signal |
|---|---|---|---|---|---|
| ↑ | ↑ | ↑ | 3 | 1 | δ + 3/2 J |
| ↓ | ↑ | ↑ | 1 | 3 | δ + 1/2 J |
| ↑ | ↓ | ↑ | |||
| ↑ | ↑ | ↓ | |||
| ↑ | ↓ | ↓ | -1 | 3 | δ - 1/2 J |
| ↓ | ↑ | ↓ | |||
| ↓ | ↓ | ↑ | |||
| ↓ | ↓ | ↓ | -3 | 1 | δ - 3/2 J |
Il s'ensuit que sur l'ensemble des molécules présentes dans l'échantillon, le proton étudié verra une fois ses trois voisins dans les états tous parallèles ou opposés au champ, et trois fois avec un des noyaux dans l'état opposé aux autres. Ainsi, son signal se présentera sous la forme d'un quadruplet avec des intensités relatives 1 :3 :3 :11. L'influence de ces voisins se caractérise par une constante de couplage J indépendante, du fait de son origine, du champ externe appliqué. En fonction de l'allure du signal d'un atome (sa figure de couplage) il est possible de connaître son nombre de voisins, ainsi que certaines indications en fonction de la valeur de la constante J2. Notons que les constantes de couplage ne concernent pas que les plus proches voisins, elles diminuent généralement avec le nombre de liaisons entre les deux atomes considérés (par exemple les constantes évoquées ci-dessus sont des constantes 3J). Au-delà de 3 liaisons, sauf cas très particuliers, ces constantes deviennent négligeables.
Pour illustrer cela, nous pouvons étudier le spectre proton de l'acétate d'éthyle :
A δ = 4,1 ppm, nous observons un quadruplet, correspondant aux protons de (2), montrant la présence de trois autres protons sur le carbone adjacent, avec une constante de couplage J = 7,04 Hz. Le déplacement chimique assez élevé montre que nous sommes à côté d'un groupe électroattracteur, ici, un oxygène. Le signal correspondant aux protons du méthyle (3) se situe à δ = 1,24 ppm sous la forme d'un triplet du fait de la proximité des deux protons de (2). Le déplacement chimique de (1) est caractéristique des protons des chaînes alkyles classiques. Le méthyle de l'acétate se présente sous la forme d'un singulet puisque le premier atome magnétiquement actif est situé cinq liaisons plus loin ; son déplacement chimique est intermédiaire entre le méthyle (3) et le méthylène (2) du fait de la présence de la fonction ester qui attire moins les électrons qu'un oxygène.
Description de l'appareillage utilisé en RMN
D'un point de vue technique, la prise d'un spectre nécessite un matériel relativement complexe du fait de la faible intensité du phénomène mis en jeu. L'échantillon est préparé dans un tube en verre borosilicaté dans un solvant dépourvus, si possible, d'atomes correspondant à l'isotope étudié. Par exemple, le solvant de choix pour l'étude des spectres protons est le chloroforme deutérié CDCl3. Son choix est issu de plusieurs avantages : le proton du chloroforme est facilement échangé par un deutérium, il est donc peu cher et de plus, le deutérium résonnant à une fréquence différente du proton, il est utilisé pour stabiliser le champ magnétique extérieur, aussi bien dans le temps (stabilité) que dans l'espace (homogénéité). Ces deux aspects du champ sont importants puisque compte tenu de la nature extrêmement ténue du signal, une variation spatiale et/ou une dérive temporelle provoqueront un élargissement important des signaux risquant de faire disparaître les figures de couplage.
La sensibilité d'une expérience de RMN s'améliore avec l'accroissement du champ magnétique ce qui nécessite l'utilisation d'aimants supraconducteurs. Ils permettent de faire circuler un courant très intense (de plusieurs dizaines d'ampère) dans un circuit de résistance nulle. Ainsi aucune perte d'énergie par dissipation thermique n'est à déplorer, alors qu'une bobine en cuivre dans les mêmes conditions dégagerait une énergie qui la ferait fondre ! Le prix à payer est qu'à l'heure actuelle, la plupart des matériaux supraconducteurs ne le sont qu'en dessous d'une certaine température (dite critique) qui est très faible (de l'ordre de -270 °C), ce qui nécessite l'emploi d'hélium liquide (qui bout à -269 °C). Afin d'assurer un minimum de perte thermique, celui-ci est calorifugé à l'aide d'azote liquide (bouillant à -196 °C).
Pour observer le phénomène de résonance, il faut un système permettant d'exciter les spins et capable de détecter la réponse de ceux-ci. Le dispositif permettant ce dialogue s'appelle une sonde.
Il existe deux types de sondes en fonction de la manière dont sont enregistrés les spectres. La méthode classique consistait à balayer la plage de fréquence que l'on désirait étudier, ce qui nécessitait de pouvoir émettre et recevoir en même temps des signaux, sans que ceux-ci interfèrent. La sonde comportait alors, entre autres, deux bobines d'axes orthogonaux à la direction du champ appliqué : une pour l'émission excitatrice et une seconde, d'axe orthogonal à la première pour la réception. Le gros inconvénient de cette technique est qu'il faut beaucoup de temps pour enregistrer un spectre, puisque le balayage doit être lent pour permettre aux spins des noyaux de revenir dans leur état d'équilibre avant de changer la fréquence. C'est pourquoi au début des années 70 est apparue une autre technique qui est beaucoup plus rapide, sensible, et qui est aujourd'hui la seule utilisée.
Cette technique est tout à fait différente puisqu'elle excite toutes les résonances (du moins dans la zone de fréquence étudiée) à la fois puis détecte le signal correspondant aux différents noyaux. Ce processus est à rapprocher de celui qui consiste à taper violemment sur une cloche puis à enregistrer le son qu'elle émet ensuite. Dans cette situation, nous n'avons plus besoin que d'une bobine pour exciter les spins et capter le signal.
La sonde peut alors se décomposer en deux parties : une partie de mesure proprement dite, composée de deux bobines, la première étant utilisée pour exciter les noyaux puis pour mesurer le signal, la seconde, facultative, permet d'irradier en permanence les résonances d'un noyau autre que celui observé. Le spectre de ce dernier est alors simplifié puisque tout effet de couplage avec le noyau irradié est supprimé (technique de découplage). La seconde partie de la sonde est constituée d'une électronique passive délicate à ajuster, pour que les bobines décrites ci-dessous présentent une efficacité maximale(comme l'accord d'un récepteur radio permet de capter une station avec un minimum de bruit).
Le rôle de cette électronique est multiple : dans un premier temps, elle sert à générer le signal d'excitation, aussi bien sa forme, que sa durée, son intensité ou sa fréquence (il s'agit de l'onde électromagnétique dont il a été question plus haut ou plutôt de son champ magnétique qui est créé par la bobine d'émission/réception). Puis elle acquiert la réponse du système de spins (signal RMN), l'amplifie, la démodule1 par rapport à la fréquence de travail du spectromètre (proche des fréquences de résonance) de manière à se ramener à des signaux basse fréquence qui seront plus facilement et plus précisément numérisés. A une translation de fréquence près, ces signaux représentent bel et bien la réponse du système de spins (fonction du temps) à laquelle on applique (sous forme numérique) une opération mathématique appelée Transformée de Fourier. Cette dernière fournit une fonction qui n'est autre que le spectre conventionnel et joue par conséquent le rôle d'analyseur de fréquence (ce que, s'il s'agit d'ondes sonores, notre oreille fait très bien séparant, par exemple, les différentes voix d'un chœur !).
Comme nous pouvons le voir, l'électronique nécessaire est complexe. Mais ces techniques, dites à Transformée de Fourier, ont permis un essor considérable de la résonance magnétique nucléaire, dans un premier temps en réduisant la durée des mesures, puis, en fonction de la préparation du système de spins, en rendant possible la détermination de propriétés moléculaires, par exemple, la manière dont sont liés les carbones entre eux dans la molécule ou quel proton est lié à quel carbone, ou encore combien de protons sont attachés à quel carbone…
Conclusion
Dans ce court dossier, nous espérons avoir montré les principes de la RMN, ainsi que son utilisation pour le chimiste et enfin la partie technique qui est souvent masquée. Nous avons ici opté pour une description n'utilisant pas l'outil mathématique et se basant sur l'expérience de phénomènes similaires courants. Toutefois, il faut noter que tout n'est pas aussi immédiat, mais qu'une étude rigoureuse, aussi simple soit-elle, nécessite des outils mathématiques et des concepts physiques très éloignés de la vie de tous les jours.
Références bibliographiques pour approfondir :
- Nuclear Magnetic Resonance.. Oxford Chemistry Primers N°32.
- La RMN. Concepts et méthodes. InterEditions. 1991.
- Identification Spectrométrique de composés organiques.. DeBoeck Université. 1998.