La chimie est une science expérimentale. Elle prédit des comportements de la matière qui doivent pouvoir être vérifiés par l'expérience. Pour accéder aux grandeurs qui caractérisent la matière, le chimiste doit faire des mesures. Il est important de connaître l'incertitude des mesures selon ce que l'on veut faire des résultats.
Pourquoi a-t-on besoin des incertitudes au laboratoire ?
La chimie est une science expérimentale. Elle prédit des comportements de la matière qui doivent pouvoir être vérifiés par l'expérience. Pour accéder aux grandeurs qui caractérisent la matière, le chimiste doit faire des mesures. Il est important de connaître l'incertitude des mesures selon ce que l'on veut faire des résultats.
Pour faire une mesure, on utilise un instrument. Ce que fait l'instrument c'est établir une correspondance entre 2 grandeurs : la grandeur mesurée et la grandeur lue.
Exemple : quand on mesure une volume avec une éprouvette, on mesure en fait la hauteur du liquide dans le récipient ; quand on mesure une température avec un thermomètre, on mesure en fait la hauteur de mercure dans le thermomètre, quand on mesure un pH, on mesure en fait une différence de potentiel entre 2 électrodes. Cette correspondance pouvant être imparfaite, on commet alors une erreur sur la grandeur qu'on veut mesurer.
L'expérimentateur peut aussi être source d'erreur : soit en lisant mal la valeur donnée par l'instrument, soit par des manipulations imprécises en mesurant une grandeur perturbée (exemple : lire un volume dans une burette contenant une goutte au robinet).
Enfin, selon les conditions (notamment température et pression) dans lesquelles on réalise l'expérience, les valeurs des grandeurs sont susceptibles de changer, ainsi que l'étalonnage des instruments (exemple : dilatation d'une pipette à haute température).
Au final, les erreurs commises lors d'une mesure ont trois origines : l'instrument, l'expérimentateur et les conditions d'expérimentation.
Ces erreurs sont de deux sortes :
- les erreurs aléatoires qui interviennent à chaque mesure et dont le sens par rapport à la valeur vraie est imprévisible. Ce sont ces erreurs qui sont traitées dans les calculs d'incertitudes ;
- les erreurs systématiques qui font apparaître un écart toujours dans le même sens par rapport à la valeur vraie. Elles sont souvent causées par le mauvais étalonnage d'un instrument.
Sachant cela, il est maintenant utile de savoir de combien on se trompe quand on effectue une mesure.
Comment donner le résultat d'une mesure ?
Donner le résultat d'une mesure, c'est en fait donner 2 nombres : une estimation de la grandeur mesurée et une estimation de l'erreur que l'on commet. Cette erreur est appelée incertitude.
Le résultat X de la mesure est donné de la façon suivante : X + U(X) avec : U(X) l'incertitude sur X.
Des méthodes particulières ont en conséquence été mises au point afin de calculer ces incertitudes et d’avoir une certaine fiabilité quant aux résultats obtenus.
Tout d’abord, il s’agit de savoir à quel type d’incertitudes on doit recourir. En effet, les incertitudes liées à une mesure unique et à une série de 100 000 mesures sont sensiblement différentes.
Incertitudes de type A (moins utilisées a priori pour les cours de chimie)
Les incertitudes de types A sont utiles quand un grand nombre de mesures sont réalisées (dans les mêmes conditions). C'est souvent le cas lorsque l'on ne dispose que de peu d’informations sur les sources d’erreurs, puisque celles-ci n’entrent pas en compte dans le calcul.
Cela permet d’ignorer l’effet des erreurs aléatoires, dont on estime qu’elles se compensent en moyenne, mais pas les erreurs systématiques, dont il faut toujours tenir compte.
Il s’agit alors d’un simple traitement statistique des erreurs : on calcule l’écart type de la série, ce qui nous donne directement l’incertitude sur la mesure.
Ecart type (= incertitude dans le cas d'une estimation de type A) :
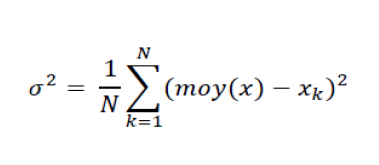
Où N : nombre de mesure effectuées ; xk : résultat de la k-ième mesure ; moy(x) : moyenne de x sur l’ensemble des mesures ; σ : écart type.
En fait, on veut calculer l’écart des valeurs vis-à-vis de la moyenne ( moy(x) – x ), mais en moyennant cela, on obtiendrait zéro, donc on met cette valeur au carré pour la rendre toujours positive (en conséquence de quoi il faut prendre au final la racine).
De cette façon, nous avons pu déterminer l’incertitude sur la valeur finale, à mesurer.
Souvent il est intéressant d'avoir un intervalle de confiance c'est-à-dire un intervalle pour lequel on a une idée de la fiabilité du résultat. Pour cela, on élargit l’incertitude en lui appliquant un coefficient k. Dans la plupart des cas, ce coefficient vaut 2 si on veut une fiabilité de 95 % et 3 pour une fiabilité de 99 %. On l'applique aussi régulièrement dans le cas des incertitudes de type B.
Vous remarquerez que lors du calcul de l'écart type, on somme des « distances » à la moyenne. Or la moyenne qui provient des mesures n'est pas la valeur vraie. L'écart-type est donc biaisé.
Pour corriger ce problème, on peut utiliser une autre formule :
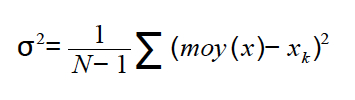
Vous vous demandez d'où vient cette formule ? Faites donc un tour en annexe !
Incertitudes de type B
Il est parfois difficile de faire une grande série de mesures, notamment si les conditions sont difficilement reproductibles ou si chaque mesure prend un certain temps. Dans ces cas-là, l’expérimentateur ne peut pas se permettre de négliger les sources d’erreurs.
Il a donc recours à des calculs de type différent, en analysant toutes les sources d’erreur. C’est ce que nous allons exposer maintenant.
On peut obtenir les grandeurs de différentes manières. Soit à l’aide d’un appareil, pour obtenir « directement » une valeur, soit en utilisant des résultats intermédiaires pour les calculer
Mesure Directe
L’expérimentateur bénéficie d’un accès « direct » à la valeur de la grandeur mesurée. C'est le cas par exemple dans le cas d’une pesée à l’aide d’une balance, ou la lecture d’un volume sur une burette graduée. Nul besoin de calcul pour l’accès à la grandeur.
Dans ces cas-là, les incertitudes sont relativement faciles à obtenir.
- Si un écart est donné par le constructeur sous la forme Δc = ±h, alors l’incertitude est de la forme : h/√3
- Lecture d’une valeur : en lisant une valeur, soit sur un appareil avec des graduations, soit sur un appareil avec différents digits. Dans ce cas-là, l’incertitude est de la forme : h/2√3
Sur une burette graduée, on aurait alors une incertitude de la forme : pas de graduation/√12
Sur une balance précise au milligramme : u = 1 mg /√12
En prenant en compte l'ensemble des sources d'erreur, on exprime alors l’incertitude sur la valeur mesurée ainsi :
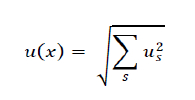
Où s représente les différentes sources d’erreurs entrant en jeu lors de la mesure de cette grandeur particulière.
On peut considérer que les différentes contributions à l’incertitude « s’additionnent , c'est à dire que l'on assimile ce cas à une mesure indirecte (cf. ci-dessous), où on aurait : Xf = Xi1 + Xi2 +… On peut retrouver cette formule en appliquant le calcul présenté en annexe.
Mesure Indirecte
Dans ce cas, un calcul est nécessaire afin d’accéder à la grandeur recherchée. En chimie il s’agit souvent de calculs du type : C2 = C1 x V1/V2
Où toutes les grandeurs en jeu sont sous forme de facteur. Dans ce cas-là, on détermine l’incertitude sur le résultat final (ici C2) à l’aide des incertitudes sur les résultats intermédiaires (ici C1, V1, V2), souvent obtenus par la méthode sur les incertitudes liées aux mesures directes.
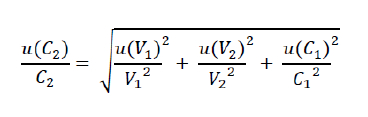
Pour plus d’informations quant à cette méthode et à ses « origines » mathématiques, se référer à l’annexe.
Pour l'incertitude de type B, il est possible d'ajouter un coefficient d'élargissement (voir paragraphe sur les incertitudes de type A).
Que dire des chiffres significatifs ?
En résumé, le résultat d'une mesure comprend deux nombres : la valeur estimée et l'incertitude. Comment relier les chiffres significatifs à la notion d'incertitude ?
Intuitivement, « plus on donne un résultat avec de chiffres significatifs, plus on est sûr du résultat ». Le nombre de chiffre significatifs est donc porteur d'une information sur l'incertitude du résultat. Lorsqu'on donne un résultat sous la forme d'un seul nombre, ce sont par convention les chiffres significatifs qui donnent la valeur de l'incertitude.
Exemple :
« Le pH est de 6,0 » (2 chiffres significatifs) se comprend comme : 5,95
« Le pH est de 6 » (1 chiffre significatif) se comprend comme : 5,5
On remarquera que quel que soit le nombre de chiffres significatifs du résultat, lorsqu'on donne une incertitude elle comporte généralement 2 chiffres significatifs tout au plus. En effet, l'ordre de grandeur de l'incertitude est généralement très inférieur à celui du résultat. Cela entraîne que des chiffres significatifs à partir du 3e correspondraient à des écarts inaccessibles aux instruments de mesures utilisés pour mesurer la grandeur. Ils ont donc peu de sens.
Lorsqu'on donne un résultat qui provient d'un calcul, il est logique de ne donner à ce résultat jamais plus de chiffres significatifs que le terme du calcul qui en compte le moins.
Exemple d'application du calcul d'incertitude : dosage de la dureté d'une eau par la méthode de MOHR
Illustrons un calcul d'incertitude sur un exemple pratique : le dosage de la dureté d'une eau.
Le protocole est le suivant :
20 mL d'eau minérale prélevés à la pipette sont tamponnés à pH = 10 à l'aide d'un tampon ammoniacal. Les ions calcium et magnésium de l'eau sont titrés par une solution d'EDTA à 1,0.10-2 mol/L. L'équivalence est détectée par un changement de couleur grâce au noir ériochrome T (NET : indicateur coloré).
Détermination de type A de l'incertitude
Dans ce cadre, on doit réaliser un grand nombre de fois le dosage (par exemple avec une classe).
Voici nos résultats :
A partir de Ve, on calcule C : C = CEDTA x Ve/Vp

La moyenne est : C = 3,958 mmol/L
L'écart-type est : σ = 0,1846 mmol/L
Le résultat de la mesure est donc : C = 4,0 ± 0,18 mmol/L (le résultat est à 2 chiffres significatifs car les données sont à 2 chiffres significatifs).
Si l'on souhaite inclure un coefficient d'élargissement pour un niveau de confiance à 95 % (k = 2) : C = 4,0 ± 0,36 mmol/L
En utilisant la formule non biaisée, on obtient un écart : σ = 0,193 mmol/L
Le résultat de la mesure avec élargissement est alors : C = 4,0 ± 0,38 mmol/L
Détermination de type B de l'incertitude
Pour cette méthode, on n'a besoin que d'une seule mesure et de tous les facteurs susceptibles d'être une cause d'imprécision.
La mesure retenue est : Ve = 7,9 mL ce qui donne : C = 3,9 mmol/L
La mesure directe de la concentration en ions calcium et magnésium n'étant évidemment pas possible, on doit mettre en œuvre la méthode sur les mesures indirectes.
On rappelle que la concentration finale en ions Ca2+ et Mg2+ qu'on note C est :C = CEDTA x Ve/Vp avec Vp le volume de la prise d'essai.
Déterminons l'incertitude sur chaque grandeur :
- CEDTA est une donnée du fabriquant : 1,0.10-2 mol/L. D'après la convention sur les chiffres significatifs, on peut donner un encadrement de CEDTA : 9,95.10-3 mol/L < CEDTA < 1,05.10-2 mol/L.
En approximation, et en l'absence de données supplémentaires on considère une distribution rectangulaire dans cet intervalle, ce qui donne une incertitude : u(EDTA) = 0,05.10-2/√3 = 0,029.10-2 mol/L = 0,29 mmol/L
- Vp est un volume prélevé avec une pipette dont l'incertitude constructeur est donnée par l’information présente sur la pipette jaugée h = ± 0,04 mL.
L'incertitude constructeur sur Vp est donc : u(Vp) = 0,04/√3 = 0,023 mL
L’incertitude de lecture peut être due éventuellement à l’alignement du ménisque avec le trait – erreur de parallaxe – mais si la manipulation est correctement réalisée, cette erreur est négligeable devant les autres incertitudes en jeu, nous n’en avons donc pas tenu compte.
- Ve est mesurée à l'aide de la burette graduée dont l'incertitude constructeur est donnée par l’information présente sur la burette graduée h = ± 0,05 mL.
L'incertitude constructeur sur Ve est donc : u1(Ve) = 0,05/√3 = 0,029 mL
On remarquera que l'incertitude de lecture pour un instrument à digits comme une burette graduée - digit de 0,1 mL – est donc : u2(Ve) = 0,1/2√3 = 0,029 mL
En prenant donc en compte ces deux sources d’incertitude, l’incertitude sur la valeur mesurée est donc : u(Ve) = (u1(Ve)2+u2(Ve)2)1/2 = 0,041 mL
D'après la loi de composition des incertitudes :
![]()
On obtient, u(C)/C = 0,0295 soit, u(C) = 0,0295 x 3,9.10-3 = 0,12 mmol/L
Le résultat de la mesure est donc au final : C = 3,9 ± 0,12 mmol/L
En appliquant un coefficient d'élargissement pour une confiance à 95 % ( k = 2) : C = 3,9 ± 0,24 mmol/L
Bibliographie, Annexe et Ressources en Ligne
[1] Nombres, mesures et incertitudes en sciences physiques et chimiques, Groupe des sciences physiques et chimiques de l'IGEN.
[2] La Mesure ; histoire, science et philosophie, Jean Perdijon, Dunod-Universciences, 2004.
[3] https://eduscol.education.fr/physique-chimie/
[4] Guide Eurachem/CITAC, Quantifier l'incertitude dans les mesures analytiques, seconde édition.
[5] L'Actualité Chimique sur CultureSciences-Chimie : Estimation de l'incertitude de la mesure lors dun dosage en chimie
Et télécharger en version pdf : l'annexe mathématique de l'article







