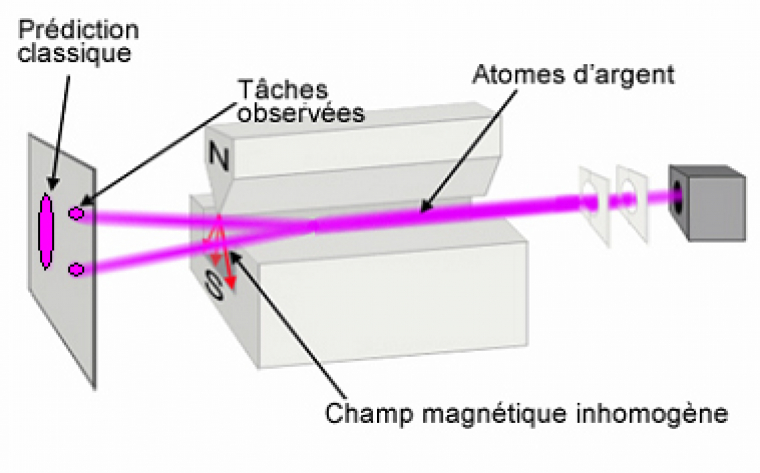
En 1922, Otto Stern et Walter Gerlach mettent en place une expérience pour déterminer si le moment cinétique électronique L est quantifié comme le propose Sommerfeld. Pour cela ils envoient des atomes d'argent à travers l'entrefer d'un électroaimant, zone où règne un champ magnétique inhomogène.
Classique ou Quantique ?
En 1922, Otto Stern et Walter Gerlach mettent en place une expérience pour déterminer si le moment cinétique électronique L est quantifié comme le propose Sommerfeld. Pour cela ils envoient des atomes d'argent à travers l'entrefer d'un électroaimant, zone où règne un champ magnétique inhomogène.
Quel est le résultat attendu ? Dans la description classique, l'électron est une particule ponctuelle en rotation autour du noyau. Cela lui confère un moment magnétique $\vec{μ}$ proportionnel à son moment cinétique $\vec{L}$ : $\vec{μ}=e/2m\vec{L}$. On peut montrer que si le gradient de champ est orienté suivant Oz dans l'entrefer, alors la force exercée sur les atomes est $\vec{F} = μ_{z} \vec{grad(B_{z})}$. Elle est orientée suivant l'axe Oz et on s'attend à voir les atomes dévier le long de l'axe Oz. Dans l'hypothèse classique, L, donc μz, prend des valeurs continues et à l'entrée de l'entrefer la répartition des moments des atomes du jet est isotrope (toutes les valeurs de -μ à +μ sont réalisées). On s'attend donc à observer une tache centrée sur l'axe du jet et allongée suivant Oz.
Le résultat expérimental est complètement différent : on n'observe que deux petites taches symétriques (cf. figure 1). La conclusion de Stern et Gerlach est que la valeur de L est quantifiée et prend dans le cas de l'argent deux valeurs opposées. Nous savons aujourd'hui que cette conclusion est fausse (il faudra attendre quelques années avant de déterminer la valeur L = 0 pour l'argent). Toutefois, cette expérience met en évidence que la propriété mesurée est quantifiée.
Naissance du spin
Quelques années plus tard, la théorie quantique alors en plein essor prend désormais en compte la quantification de la norme du moment cinétique orbital $\vec{L}$ et celle d'une de ses projections, Lz, suivant la règle : Lz = mh/2π ; m ∈ [-l; +l] ; l étant un entier naturel.
Si on essaie de ré-interpréter l'expérience de Stern et Gerlach dans ce cadre nouveau, on aboutit encore à une impasse. En effet, si la déviation du jet est bien due à l'interaction B - L, alors on doit observer un nombre impair de taches ! Il faudra attendre encore pour obtenir une interprétation satisfaisante de l'expérience.
En 1925, pour rendre compte des spectres atomiques, notamment le dédoublement des raies spectrales du sodium, Georg Uhlenbeck et Samuel Goudsmith proposent une hypothèse : les électrons sont pourvus de "spin" (de l'anglais "to spin" , tourner). Ils formulent l'image classique d'un mouvement de rotation autour de l'électron autour de son axe, ce qui lui confère un moment magnétique intrinsèque1. L'électron est une particule de spin 1/2 et la projection du spin sur un axe ne prend pas de valeurs continues mais seulement deux valeurs qui sont multiples de la constante de Planck : +1/2 (spin up) et -1/2 (spin down).
Relecture de l'expérience
L'expérience de Stern et Gerlach sera ré-interprétée en terme de spin électronique en 1927. À cette date, la configuration de l'atome d'argent (ZAg = 47) est établie : [1s22s22p63s23p63d104s24p64d10]5s1.
On sait également qu'une couche pleine ne contribue pas au moment cinétique orbital et que l'électron de l'état 5s a un moment cinétique orbital nul (pour une sous-couche s, on a l = 0), donc la seule contribution au moment magnétique est le spin des électrons. De plus chaque paire d'électrons occupant un état a un spin total nul. Il ne reste plus que le spin de l'électron occupant l'état 5s. Ce sont donc les deux états du spin qui correspondent aux deux taches observées au cours de l'expérience de Stern et Gerlach. C'est une nouvelle confirmation expérimentale de la valeur du spin électronique S = 1/2.
Conclusion
On peut remarquer que le spin électronique est introduit historiquement comme un paramètre supplémentaire indispensable pour interpréter des résultats expérimentaux. C'est donc un postulat de la théorie. En 1928, Paul Dirac formule une approche relativiste de la mécanique quantique au sein de laquelle l'existence découle des postulats de base.
Biographies
Otto Stern (1888-1969), physicien allemand, professeur à l'Université de Hambourg, à l'Institut de Technologie de Carnegie et à l'Université de Berkeley. Il utilise les faisceaux moléculaires pour mesurer les propriétés magnétiques des molécules et des protons et détermine ainsi les moments magnétiques de l'électron et du proton. Prix Nobel de physique en 1943.
Walter Gerlach (1889-1979), physicien allemand, professeur aux universités de Tübingen et Munich. Il effectue avec Otto Stern l'expérience qui porte leurs noms et qui montre que le moment magnétique de l'électron ne prend que des valeurs discrètes. Il apporte aussi une contribution à la physique du rayonnement, à la spectroscopie et à la physique quantique.
Georg Uhlenbeck (1900-1988), physicien américain d'origine hollandaise, professeur aux universités d'Utrecht, Michigan et New York. Avec Goudsmith, il introduit le spin de l'électron pour expliquer les résultats des expériences de Stern et Gerlach. Il apporte une contribution à la physique atomique, à la physique nucléaire et à la mécanique quantique.
Samuel Goudsmith (1902-1978), physicien américain d'origine hollandaise, membre des MIT Radiation Laboratory et Brookhaven National Laboratories, professeur à l'Université de Reno. Avec son collègue Georg Uhlenbeck, pendant leur doctorat à l'université de La Haye, il émet l'hypothèse du spin de l'électron. Pendant la Seconde guerre mondiale, il travaille sur les ondes radar au Radiation Laboratory du MIT et est le chef d'une mission secrète d'évaluation du progrès allemand dans la construction de la bombe atomique.
Paul Adrien Maurice Dirac (1902-1984), physicien anglais, professeur à l'Université de Cambridge. Il montre que le formalisme de la mécanique quantique d'Heisenberg et celui de Schrödinger sont équivalents, introduit la relativité restreinte dans la mécanique quantique en postulant l'équation qui porte son nom (cette équation décrit le spin et les antiparticules), postule le monopole magnétique et propose la statistique quantique des fermions (appelée Fermi-Dirac). Prix Nobel de physique en 1933.
Bibliographie et ressources en ligne
1] C. Cohen-Tannoudji, B. Diu, et F. Laloë, Mécanique Quantique, volume I, Hermann, Paris, 1992, p 386-390.