Quatrième opus du dossier consacré à la cristallographie, cet article traite de la diffraction des rayons X par un cristal, plus précisément de l'aspect technique.
Techniques expérimentales
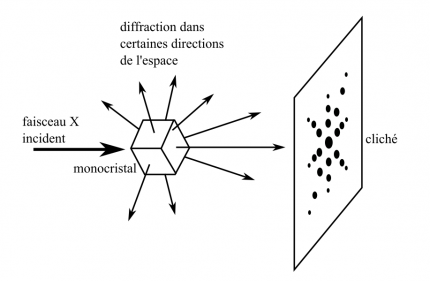
Un cristal exposé à des rayons X diffracte le faisceau dans différentes directions. Les directions des faisceaux diffractés sont une mine d’informations, puisqu’elles sont reliées directement à la structure du cristal via la loi de Bragg.
De très nombreuses techniques d’étude des cristaux par rayons X ont été développées au cours du XXe siècle. Toutes reposent sur un même principe : trouver dans l’espace les faisceaux de rayons X ayant été diffractés par le cristal et relier leur position aux familles de plans réticulaires associées.
L’enjeu est donc de développer des dispositifs permettant l’acquisition d’un diffractogramme aussi complet que possible afin d’avoir un maximum de données pour élucider la structure cristalline.
Nous allons vous présenter ici certaines méthodes de collecte, qui nous semblent les plus intéressantes du point de vue historique ou pratique.
Techniques utilisant un monocristal
Méthode de Laue
La première méthode de collecte de faisceaux diffractés a été élaborée par Max von Laue en 1911. Elle consiste à faire passer un faisceau de rayons X polychromatique à travers un cristal immobile (Figure 1). Le faisceau diffracté impressionne une plaque radiographique située derrière le cristal (Figure 2). Cette première technique a l'avantage de montrer les symétries de la structure, pourvu que le cristal soit orienté correctement, mais la résolution de structure est fastidieuse car elle nécessite un grand nombre d'acquisitions. En effet, dans la grande majorité des cas, toutes les symétries ne peuvent apparaître sur un même cliché. De plus, l’image étant très déformée, il est très difficile d’indexer la figure de diffraction, c’est-à-dire de faire correspondre une tache à la famille de plans réticulaires l’ayant diffractée.
On voit bien la symétrie d'ordre 4 et les miroirs.
Chambre de Weissenberg
Cette technique a été mise au point par Karl Weissenberg dans les années 30.
Le faisceau incident est désormais monochromatique, ce qui augmente la résolution de l’image, mais nécessite la mise en mouvement du cristal pour mettre de nombreux plans réticulaires en conditions de diffraction.
Le cristal est placé en rotation autour de l’axe d’une chambre cylindrique. Au cours de l’acquisition, le cylindre, qui porte un film photographique sur ses parois, subit également une translation le long de cet axe (Figure 3). On limite ainsi la superposition des taches, ce qui rend un sens à l’intensité de la tache et l’indexation est grandement facilitée grâce à des abaques calculés. En faisant plusieurs acquisitions avec des orientations du cristal différentes, toutes les taches observables sont visibles. Cependant, la figure de diffraction est plus complexe et les symétries ne sont pas apparentes.
Cette méthode révolutionna la résolution de structures en son temps et fut utilisée jusque dans les années 1950, où d’autres méthodes plus perfectionnées furent mises au point.
Pour un cliché, l’un des indices de Miller est fixé. Le long des droites, un seul indice varie. Le long des courbes, comme la courbe bleue, les deux indices varient. Par exemple, le long de la droite marron se trouvent les réflexions sur des plans réticulaires d'indices (h10) où seul h varie.
Sur la Figure 4, on peut remarquer l’absence de certaines taches. La plupart du temps ces extinctions sont dues à une symétrie translatoire ou à une maille non primitive et sont appelées extinctions systématiques, comme nous l’avons montré précédemment dans le cas du fer α, cubique centré.
Par exemple, dans le cas de NaCl, en choisissant h = 1, k = 0, et l = 0, le facteur de structure est nul (cf. III, 4), donc l’'intensité de la tache est nulle. Plus généralement dans le cas d’une maille cubique à faces centrées, les taches sont observées si h, k et l sont de même parité.
Quatre cercles
Le diffractomètre à quatre cercles (Figure 5) est le plus utilisé pour la résolution de structures complexes, comme les cristaux de protéines. Il nécessite l’emploi d'un monocristal d'environ 100 µm. C’est une extension de la méthode de Laue, mais le cristal est mis en rotation suivant trois axes et le détecteur suivant un axe, afin d’obtenir en une acquisition un maximum de taches. Le traitement des données est fortement automatisé.
Remarque : à l’heure actuelle, les appareils de diffraction des rayons X n’utilisent plus de films photographiques mais des détecteurs permettant de mesurer l’intensité du faisceau diffracté.
Diffraction de poudres
L’obtention d’un monocristal peut être un véritable défi voire une gageure. C’est pourquoi des méthodes de diffraction sur des poudres ont été mises au point. Ces techniques sont très utiles pour l’identification des phases et l’ajustement des paramètres de maille et des positions atomiques d’une phase déjà connue et résolue. Leur avantage est de recueillir toutes les données en une seule acquisition, puisque statistiquement, dans une poudre suffisamment fine, toutes les orientations de cristal sont présentes (mais pas forcément équiprobables), et il est donc a priori inutile de mettre en mouvement le système. Elles peuvent donc être exploitées comme des méthodes analytiques de routine au même titre que la RMN et la spectroscopie infrarouge par transformée de Fourier (IRTF), par exemple.
Méthode de Debye-Scherrer
La poudre, insérée dans un capillaire ou englobée dans de la résine, est placée au centre d'une chambre cylindrique et exposée à un faisceau monochromatique de rayons X.
Toutes les orientations de cristal étant présentes, l’image ainsi obtenue n’est plus constituée de taches (intersection d’une droite et d’un plan), mais d’anneaux dits de Debye-Scherrer (Figure 6), par symétrie de révolution autour de l’axe d’incidence : il s’agit de l’intersection d’un faisceau de droites de même angle (donc un cône de demi-angle au sommet 2θ) avec un plan.
A gauche, une chambre de Debye-Scherrer. On notera sur les parois la présence d'un film photographique. A droite, clichés obtenus par la méthode de Debye-Scherrer. Les clichés sont pris sur cinq échantillons de laiton (alliage de cuivre et de zinc) de différentes teneurs en cuivre. On remarque la variation d’intensité de certains anneaux avec la composition, à cause de la variation de la valeur du facteur de forme f en passant du zinc au cuivre.
Méthode de Bragg-Brentano
Le diffractomètre de Bragg-Brentano (Figures 7 et 8) est le plus utilisé aujourd’hui. Le faisceau est incliné d'un angle θ par rapport au plan de la surface de l'échantillon et le détecteur est placé en face, incliné du même angle θ. Le système peut balayer des valeurs de θ comprises entre 5° et 85°. Les angles plus faibles sont difficilement accessibles car le faisceau devient rasant et le signal détecté est celui du faisceau incident. Les angles plus grands sont interdits parce que les constituants (source et détecteur) de l’appareil se gênent mutuellement. Le diffractogramme obtenu (Figure 9) est le même qu’avec la méthode de Debye-Scherrer, mais les anneaux ne sont pas visibles, car on récolte directement l’intensité en fonction de l'angle. Tout se passe comme si le détecteur parcourrait la chambre de Debye-Scherrer le long du film.
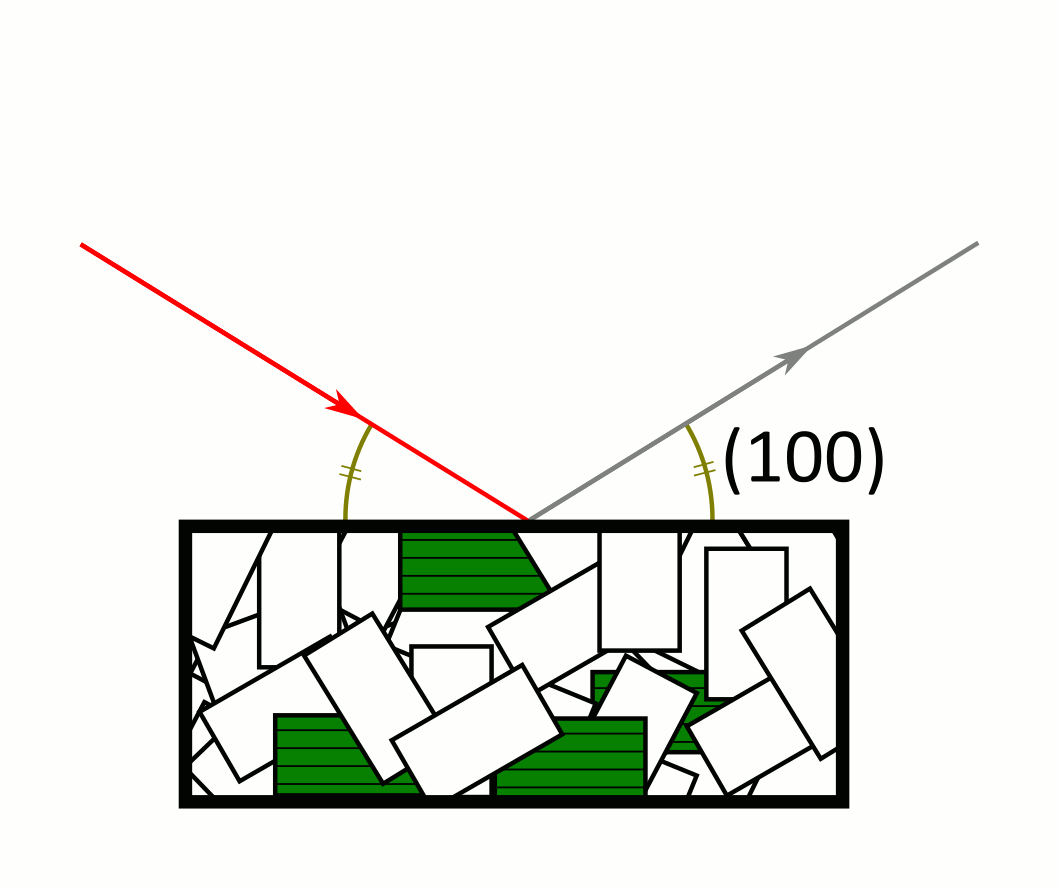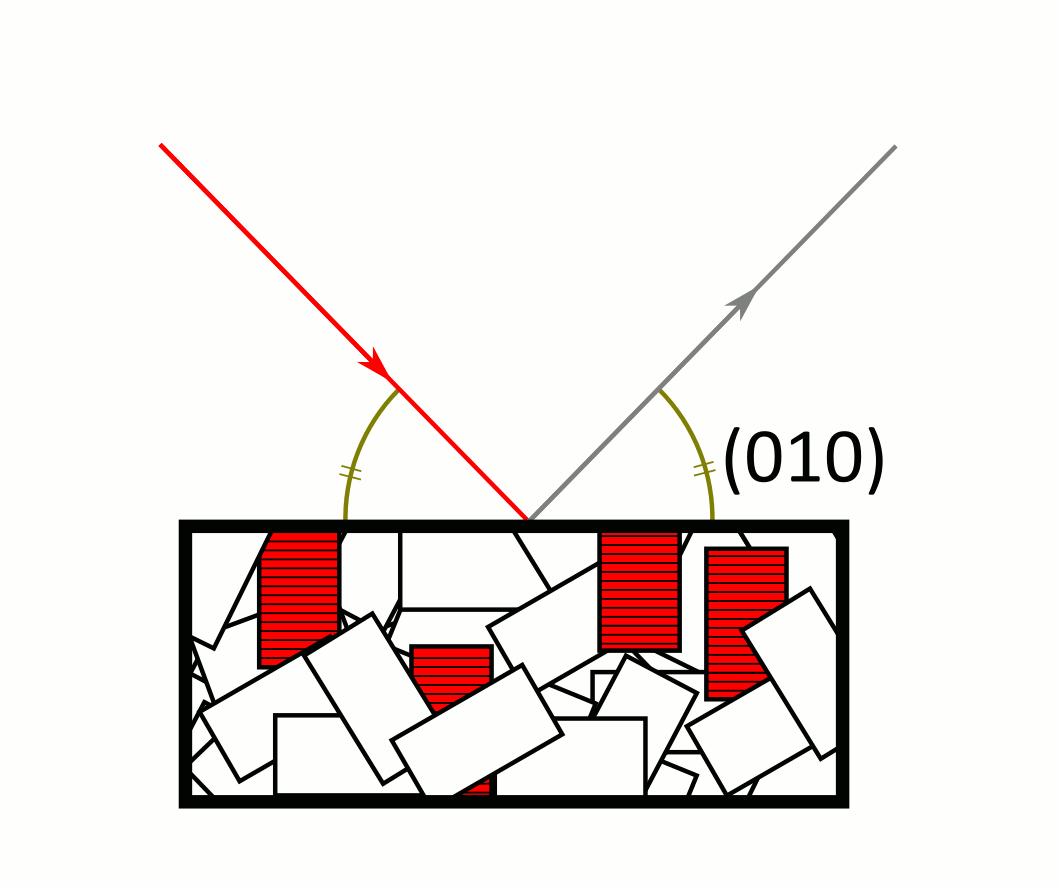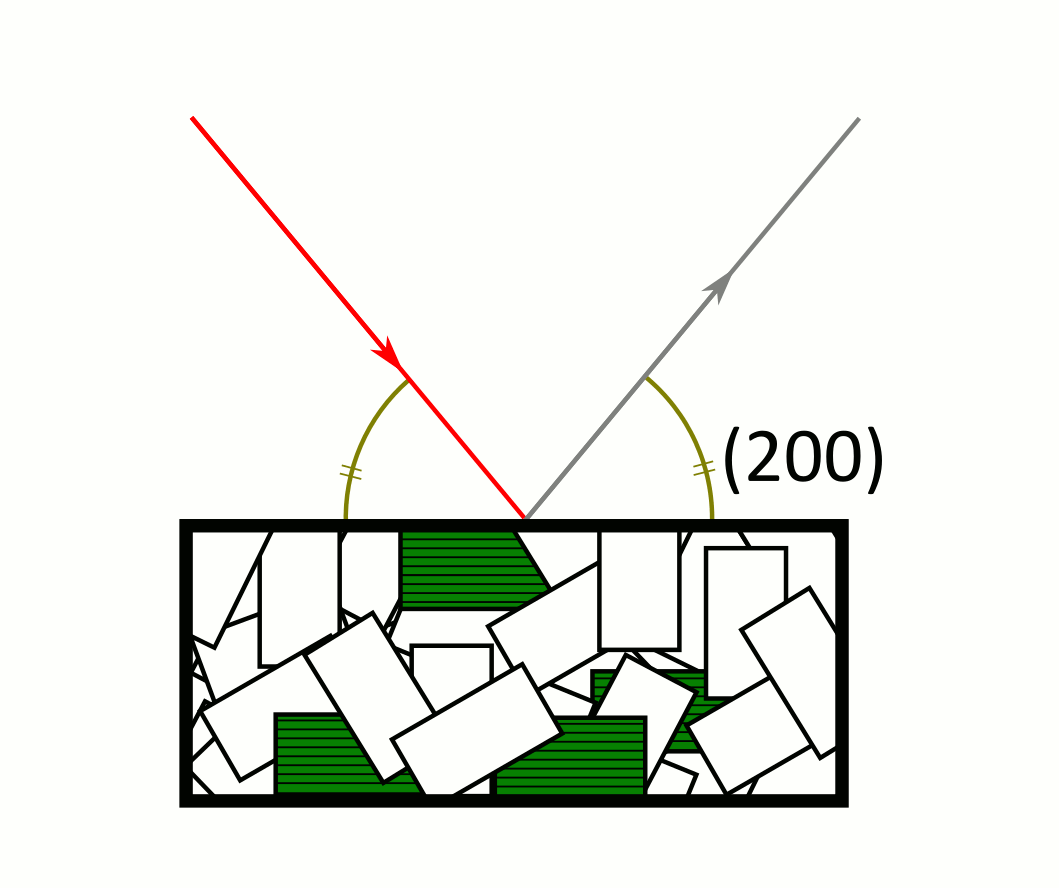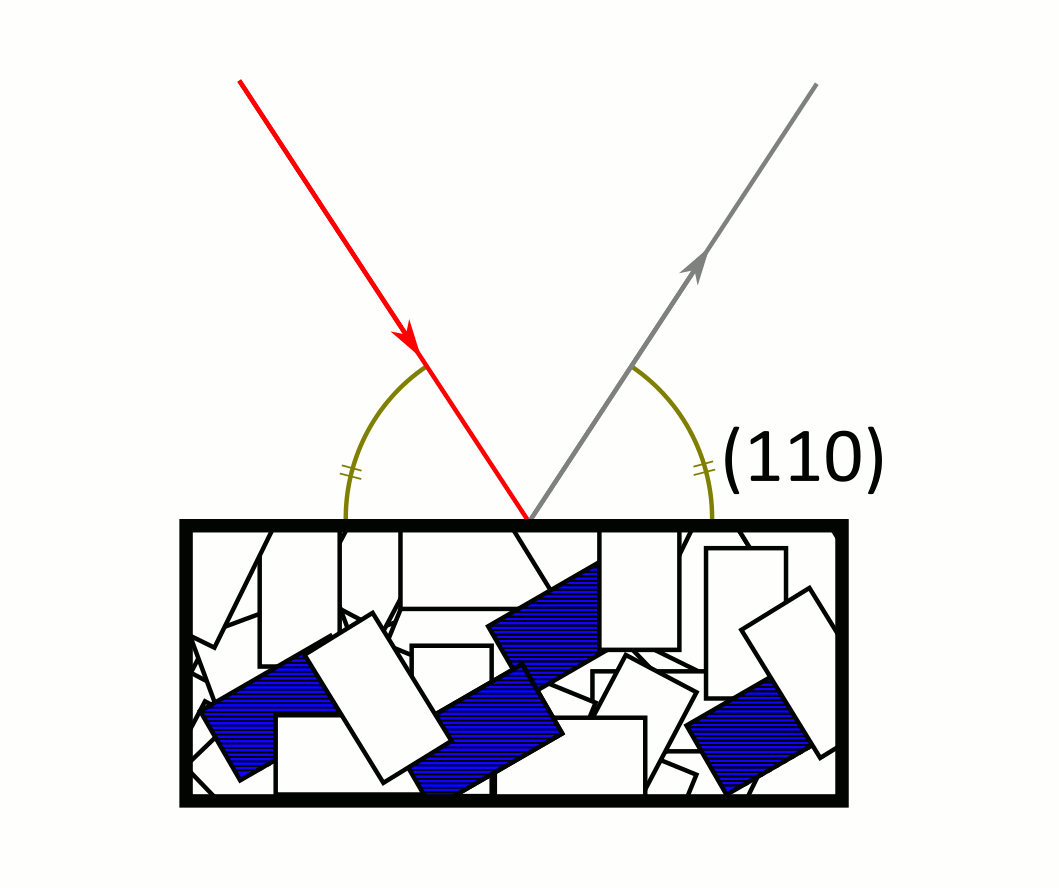
Le faisceau incident (rouge) est diffracté par les cristaux de la poudre. Le détecteur est au niveau du rayon diffracté (gris) et ne reçoit de signal que lorsque la loi de Bragg est vérifiée pour un cristal de la poudre. Les cristaux verts sont dans la bonne position pour que le faisceau diffracté par leurs plans (100) et (200) soit détecté, mais pas pour les plans (010) ni les plans (110). Le signal des plans (010) est émis par les cristaux rouges, celui des plans (110) par les bleus. Attention : les rayons gris ne sont pas les seuls rayons émis (à tout instant, l’échantillon émet les anneaux de Debye-Scherrer au complet), mais les rayons que l’on détecte.
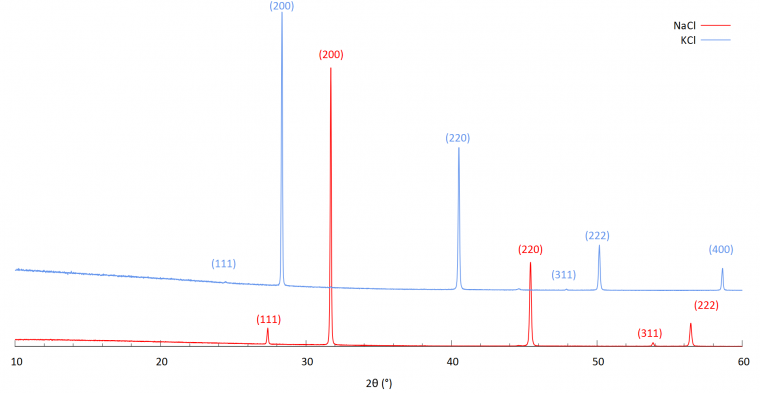
Les intensités ont été normalisées. Leurs structures présentent la même symétrie et la disposition des ions dans la maille est également identique. On remarque ainsi une correspondance entre les pics. La différence de position des pics est due à la différence de rayons ioniques entre Na+ et K+, qui modifie le paramètre de maille.
On rappelle la formule du facteur de structure pour NaCl :
$$F_{h,k,l}=\Bigg(1+\exp\left[j{\pi}(h+k)\right]+\exp\left[j{\pi}(h+l)\right]+\exp\left[j{\pi}(k+l)\right]\Bigg)\Bigg(f_{Cl}+f_{Na}\exp\left[{\pi}j(h+k+l)\right]\Bigg)$$
On note aussi que sur KCl, les pics d’indices impairs, notamment le pic (111) ont une intensité presque nulle, en effet, K+ et Cl– ont le même facteur de forme aux faibles angles, donc le facteur de structure s’annule pour des indices h, k, l tous impairs.
Analyse des résultats d’un diffractogramme
Analyse d’un diffractogramme sur poudre
Cette partie illustre sur l’exemple du chlorure de sodium NaCl, la méthode utilisée pour déterminer la structure cristalline d’un échantillon à partir de son diffractogramme sur poudre.
télécharger le texte de cette partie
Extension aux méthodes sur monocristal
Dans le cas d’une diffraction sur monocristal, la résolution de structure est facilitée par la connaissance de l’orientation du monocristal tout au long de l’acquisition et de l’obtention d’un diffractogramme bidimensionnel. Cela permet, par exemple, de distinguer les raies (100), (010), (001), (-100), (0-10), (00-1). Ainsi, on a beaucoup plus de pics, donc d’informations pour résoudre la structure. Le principe de la résolution reste quant à lui le même (bien qu’il soit facilité) : la position des raies indique la symétrie de la structure et ses paramètres de maille, l’intensité des raies permet de remonter à la nature et la position des atomes.
Pour illustrer le potentiel de la méthode, nous avons pris un échantillon d’un minéral inconnu (Figure 10).
L'image est prise à la loupe binoculaire. Le fragment est de couleur orange en lumière naturelle, il apparaît bleu ici car il est observé en lumière analysée
Après acquisition du diffractogramme en quatre cercles (Figure 11), la structure a été résolue.
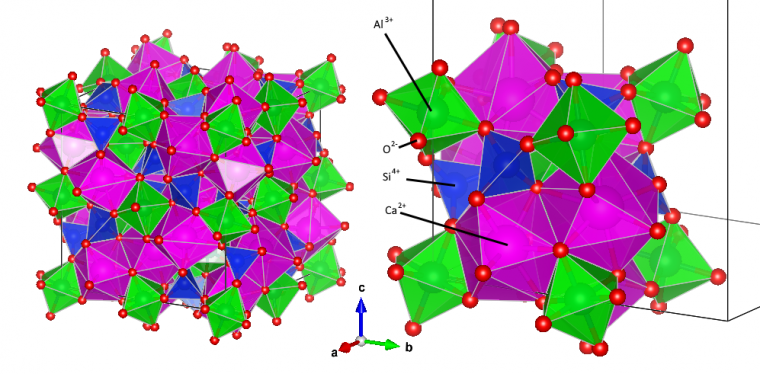
Celle-ci correspond à celle d’un grenat (Figure 12).
Maille complète à gauche; uniquement un huitième de maille à droite, qui contient une seule unité formulaire Ca3Al2Si3O12.
La structure est cubique centrée et appartient au groupe Ia-3d, avec un paramètre de maille a = 11,846 Å. Le silicium occupe des tétraèdres, l’aluminium des octaèdres, et le calcium des sites de coordinence 8 déformés. Les oxygènes sont tous équivalents, liés à un Si4+, un Al3+ et deux Ca2+. L’oxygène est à une position qui n’a rien de spécial d’un point de vue géométrique, qui est donc de multiplicité maximale pour ce groupe, c’est-à-dire 96 (il subit toutes les opérations de symétrie du groupe), tandis que les ions silicium, aluminium et calcium sont placés sur des éléments de symétrie du cristal (et ne sont donc pas affectés par les opérations de symétrie correspondantes) et se trouvent donc sur des positions de multiplicité réduite (respectivement 24, 16 et 24). Ainsi une maille contient 8 unités formulaires. Pour correspondre à la structure du grenat analysé, un ion Al3+ sur trois est aléatoirement remplacé par un ion Fe3+, et le paramètre de maille passe à a = 11,732 Å.
Plus précisément, afin d’assurer un ajustement optimal de la position des pics et de leur intensité, on doit considérer qu’il s’agit d’une solution solide de 67 % de grossulaire (Ca3Al2Si3O12) et de 33 % d’almandin (Ca3Fe2Si3O12). Ces résultats sont compatibles avec la composition mesurée via une autre technique d’analyse : l’EDS (energy-dispersive x-ray spectroscopy).
|
|
O |
Si |
Ca |
Al |
Fe |
|
%mol mesuré |
59,9±0,01 |
14,9±0,03 |
14,9±0,03 |
6,7±0,1 |
3,2±0,1 |
|
%mol théorique |
60,0 |
15,0 |
15,0 |
Somme = 100% |
|
Résultat des analyses EDS.
Conclusion
La périodicité qui caractérise l’état cristallin d’un solide fait apparaître de nombreuses et diverses opérations de symétrie qui structurent le cristal et sont à l’origine de sa forme et de ses propriétés physico-chimiques. L’une de ces propriétés est la capacité d’un cristal à diffracter les rayons X. La découverte de ce phénomène il y a plus de 100 ans a conduit à l’étude de son origine et des lois qui le régissent, qui sont apparues intimement liées à la disposition des atomes au sein d’un solide. Ainsi la diffraction des rayons X est devenue LA méthode permettant encore aujourd’hui l’étude de la relation structure-propriétés des solides cristallins et l’exploration de la structure des molécules, jusqu’aux plus complexes d’entre elles.
Bibliographie (commune aux quatre articles du dossier)
- Cours de cristallographie Livre III Première Partie Radiocristallographie Théorique, R. Gay, Gauthier-Villars et Cie, 1961.
- Symétrie et Structure, J. Angenault, Vuibert, 2001.
- Propriétés physiques des cristaux, leur représentation par des tenseurs et des matrices, J.F. Nye, Dunod, Paris, 1961.
Remerciements
Nous aimerions remercier Kamal Boubekeur pour le temps qu’il nous a consacré, pour nous avoir fourni les chambres de Weissenberg et de Debye-Scherrer, pour les clichés correspondants ainsi que pour l’utilisation du diffractomètre à quatre cercles. Nous tenons également à remercier le Grenat, sacrifié sur l’autel de la science, Sarah Gayot qui nous l’a fourni et Aisha Kanzari pour les photographies de lame mince.