Premier opus du dossier consacré à la cristallographie, cet article donne un certain nombre de définitions.
L'ONU a choisi de faire de 2014 l'Année Internationale de la Cristallographie, en commémoration du début de cette formidable épopée scientifique, à l'origine de près d'une vingtaine de prix Nobel en physique, en chimie et en médecine. La diffraction des rayons X est longtemps restée la seule méthode capable d'élucider les structures tridimensionnelles des composés chimiques, des molécules telles que l'eau ou le benzène à l'ADN, jusqu'aux protéines les plus complexes, pourvu que l’on réussisse à en faire un cristal.
La cristallographie, c’est-à-dire l’étude des édifices cristallins, naît à la fin XVIIIe siècle, lorsque l'abbé René-Just Haüy émet l'hypothèse que les cristaux sont constitués de "molécules intégrantes" qui s'empilent toujours de la même façon. Sur la base des travaux de Jean-Baptiste Romé de l'Isle, la cristallographie devient une méthode d'identification des minéraux, puis des composés chimiques en général ; elle est notamment impliquée dans la découverte de la chiralité par Pasteur. En reprenant l'idée de Haüy, Auguste Bravais imagine les différentes formes que peut prendre la "molécule intégrante" et ouvre la voie à des modèles mathématiques reposant sur les symétries. Von Laue a l'idée d'étudier l'interaction entre les rayons X (découverts par Röntgen en 1895) et les cristaux et découvre ainsi la diffraction. Reprenant tous ces acquis, William Henry Bragg et son fils William Lawrence établissent en 1913 les premières structures cristallines (notamment le diamant et NaCl) et sont récompensés par le prix Nobel de Physique dès 1915, ouvrant la voie à la résolution de structures par diffraction des rayons X.
Depuis lors, un très grand nombre de travaux utilisant des méthodes cristallographiques ou en développant des nouvelles, ont été récompensés par d’autres prix Nobel, comme en témoigne la liste fournie par l'Union Internationale de la Cristallographie. On s'attachera ici à la description des structures cristallines, puis à l'étude physique du phénomène de diffraction, avant d'étudier quelques méthodes d'analyse.
Description d'une structure cristalline
Maille, nœuds et plans réticulaires
Un cristal est un solide dont les constituants (atomes, ions, molécules) sont organisés de façon régulière ; il est traditionnellement défini par la périodicité de sa structure atomique. On peut alors identifier une sous-structure, le motif, qui est l'unité de répétition.
La définition du mot cristal a évolué au cours des siècles :
- au XVIIIe siècle, le terme cristal s’impose aux savants pour désigner toutes les pierres angulaires limitées par des faces.
- au début du XIXe siècle, le cristal désigne tous les matériaux solides homogènes limités par des faces.
- aux XXe et XXIe siècles, le cristal désigne tous les matériaux ordonnés à l’échelle atomique.
- selon l’Union internationale de cristallographie, tout solide dont le diffractogramme (voir les volets ultérieurs de la série d’articles) est essentiellement discret est un cristal. Sur la base d'une propriété structurelle essentielle, cette définition englobe les cristaux classiques mais aussi les quasi-cristaux).
Dans chaque structure cristalline, on peut identifier une infinité de motifs différents, plus ou moins complexes, qui représentent la formule brute du composé (ou un de ses multiples). On choisit par convention le motif le plus simple possible qui permette par périodicité de reproduire l’ensemble de la structure.
Chaque point sur lequel un motif est appuyé est un nœud. L'ensemble des nœuds forme un réseau (Figure 1).
Chaque occurrence du motif peut ensuite être remplacée par un nœud.
Supprimons pour l'instant le motif en ne conservant que les nœuds : nous nous intéressons donc, dans un premier temps, au réseau.
On observe alors qu'il existe des opérations de symétrie qui laissent le réseau inchangé, notamment certaines translations.
Un triplet de translations de réseau non colinéaires forme une maille, volume délimité par six faces en forme de parallélogramme, identiques et parallèles deux à deux : il s’agit d’une unité de répétition du réseau. Une fois encore, un réseau donné peut contenir une infinité de mailles, certaines ne contiennent qu'un seul nœud (les mailles primitives, Figure 1) d'autres en contiennent plusieurs (les mailles multiples, Figure 2 et 3), mais seules quelques-unes, les mailles conventionnelles, sont représentatives de la symétrie totale, ses vecteurs directeurs étant parallèles aux axes de symétrie : on travaillera toujours dans ces dernières.
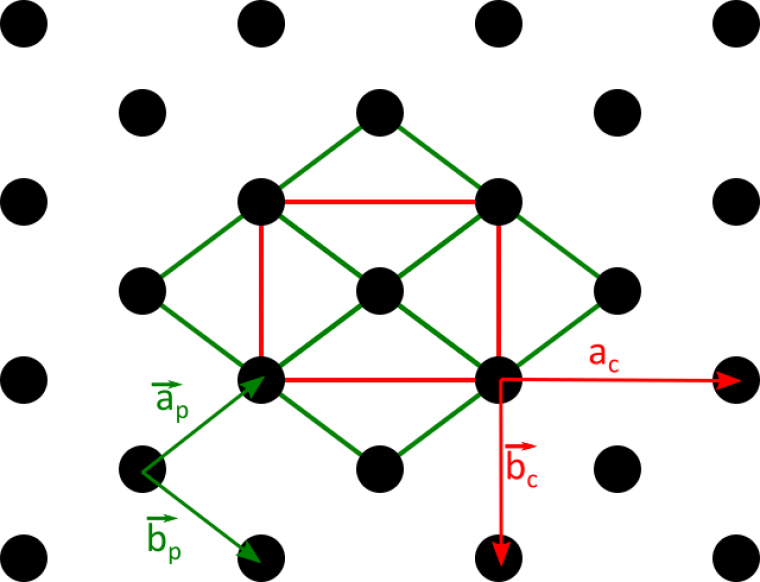
Les mailles bleue, rouge, verte et violette sont élémentaires. A partir d’une maille et de son contenu (ici on a pris la maille rouge), il est possible de reconstituer l’ensemble du pavage.
Deux mailles possibles sont dessinées. La maille verte est primitive, mais la maille rouge est la maille conventionnelle. En effet, les vecteurs $\vec{a_{c}}$ et $\vec{b_{c}}$ sont portés par des axes de symétrie contrairement aux vecteurs $\vec{a_{p}}$ et $\vec{b_{p}}$.
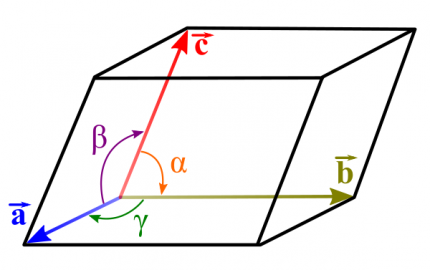
Dans le cas d’un cristal tridimensionnel, on définit ainsi un repère (Figure 4), dont les axes sont dirigés par les vecteurs $\vec{a}$, $\vec{b}$ et $\vec{c}$ formant une base directe dans laquelle sont calculées toutes les coordonnées, appelées «coordonnées réduites». Dans le cas d’une maille primitive, les nœuds du réseau ont donc des coordonnées entières.
Une maille est complètement définie par six paramètres de maille, trois pour la longueur de chaque vecteur de base $\vec{a}$, $\vec{b}$ et $\vec{c}$, trois pour les angles entre les vecteurs de base : $\alpha$ (l'angle entre $\vec{b}$ et $\vec{c}$), $\beta$ (l'angle entre $\vec{a}$ et $\vec{c}$) et $\gamma$; (l'angle entre $\vec{a}$ et $\vec{b}$).
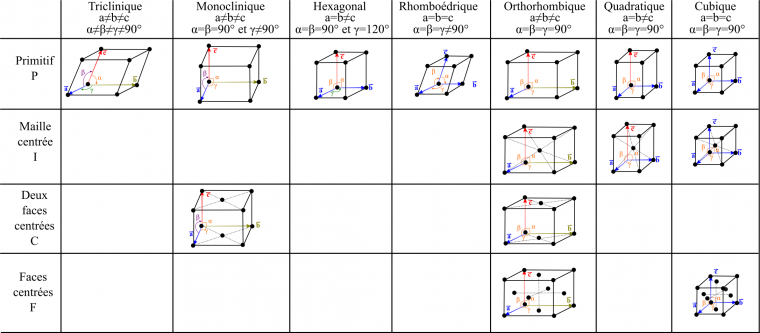
Une maille, puisqu’elle décrit une structure cristalline, doit être compatible avec la périodicité du réseau. Partant de ce principe, Auguste Bravais a démontré (Figure 5) que l’on peut définir :
- sept géométries appelées systèmes cristallins.
- quatre modes de réseau : une maille peut être primitive (P), mais aussi avoir un nœud en son centre (I); un nœud au centre de deux faces opposées (base centrée, C) ou un nœud au centre de chaque face (faces centrées, F).
- parmi les vingt-huit paires système-mode, seules quatorze, les réseaux de Bravais, sont possibles dans un cristal.
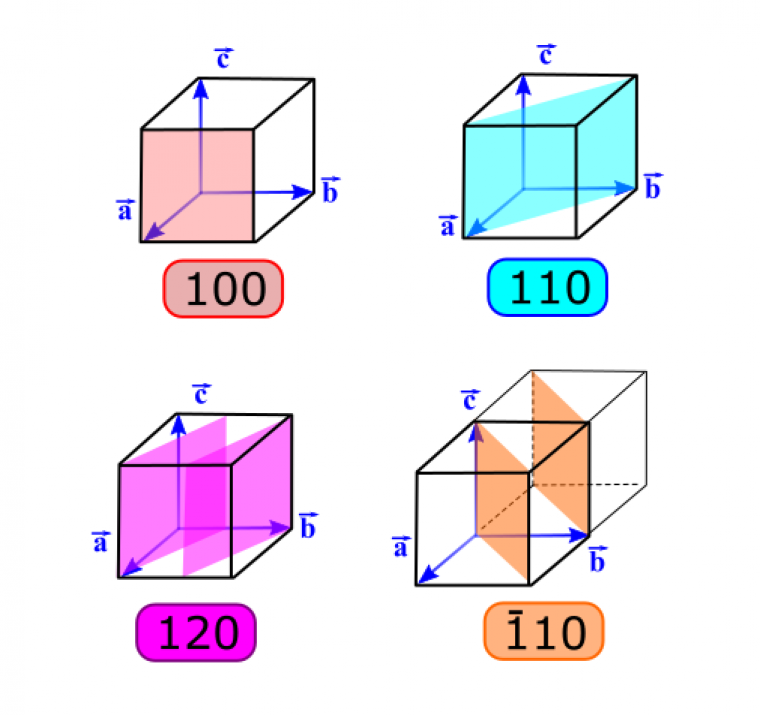
Trois nœuds non alignés du réseau définissent un plan réticulaire. Il appartient à une famille de plans réticulaires parallèles et équidistants, chaque plan ayant pour équation hx + ky + lz = m, avec m un entier relatif et h, k et l des entiers relatifs appelés indices de Miller (Figure 6).
Les plans d’une même famille sont caractérisés par les mêmes valeurs d’indices h, k et l. Au sein d’une famille de plans, le plan contenant l’origine a pour équation hx + ky + lz = 0. Le plan suivant, d’équation hx + ky + lz = 1, coupe les axes dirigés par les vecteurs $\vec{a}$, $\vec{b}$ et $\vec{c}$ respectivement aux points (1/h,0,0), (0,1/k,0) et (0,0,1/l).
En cristallographie, le signe "moins" d'un entier négatif est placé au-dessus du chiffre.
Symétries
La symétrie est l’invariance d’un objet par rapport à certaines opérations appelées opérations de symétrie. On appelle élément de symétrie l’ensemble des positions laissées invariantes par l’opération de symétrie en question. Si on se place dans une maille primitive, on peut observer quatre types d’opérations de symétries :
- les rotations d'ordre 2, 3, 4 ou 6 (une rotation d'ordre n est une rotation d'angle 2π/n autour d’un axe) ; l’élément de symétrie correspondant est un axe appelé axe n.
- les réflexions ; l’élément de symétrie correspondant est un plan appelé miroir, noté m.
- l’inversion, notée -1 ; l’élément de symétrie correspondant est un point.
- les rotations impropres ou roto-inversions, notées -3, -4 et -6, qui sont composées d’une rotation (d’ordre 3, 4 ou 6) et d’une inversion.
Remarque : dans cet article, les notations utilisées pour les opérations et éléments de symétrie sont celles d’Hermann-Mauguin.
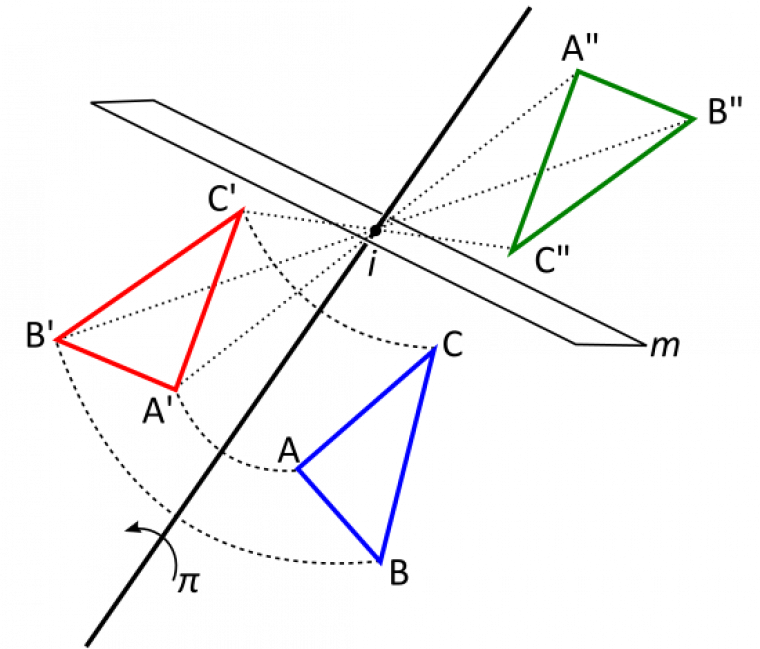
On notera que la rotation impropre d’ordre 2 (Figure 7), notée -2, qui est composée d’une rotation d’angle π suivie d’une inversion correspond en fait à une réflexion par rapport à un plan perpendiculaire à l’axe de rotation ; on la note donc fréquemment m.
Le triangle A’’B’’C’’ est l’image du triangle ABC par la rotation d’angle π suivie de l’inversion : c’est également l’image du triangle ABC par rapport au plan de symétrie m.
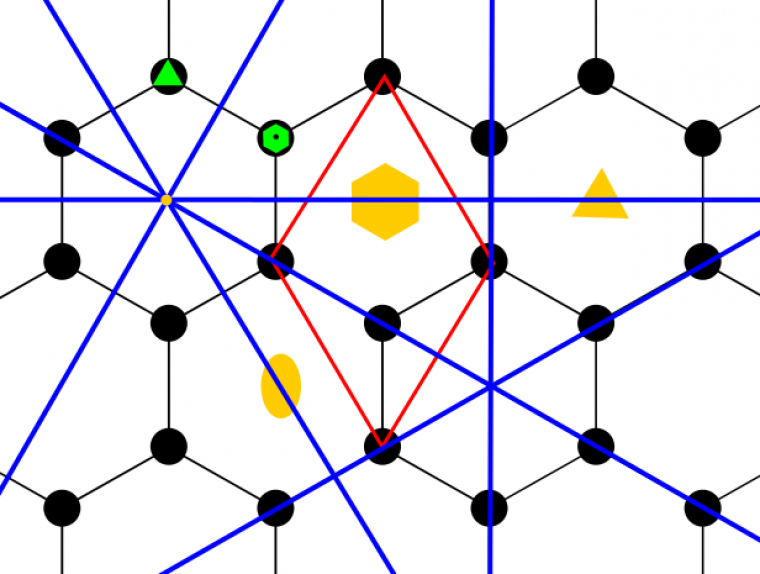
Considérons l’exemple du graphite, variété allotropique de carbone, constitué d’un empilement de feuillets bidimensionnels appelés graphènes (Figure 8).
Sur un plan de graphène, dont la maille est figurée en rouge au centre, on a :
- Au centre de chaque hexagone :
- un axe 6 (matérialisé par un hexagone jaune),
- un axe 3 (triangle jaune)
- un axe 2 (ellipse jaune)
- un centre d'inversion.
- Sur chaque atome de carbone :
- un axe d’ordre -6 (hexagone vert troué),
- qui comprend un axe 3 (triangle vert).
- Deux familles de plans miroirs (une famille contient un ensemble de miroirs équivalents par symétrie) : ceux contenant l’axe d’ordre 6 (en bleu) et d’autres correspondant aux plans de graphène.
Les axes de rotation ici représentés sont perpendiculaires au plan de l'image.
Les autres ordres de rotation sont impossibles dans un réseau périodique et ne sont donc pas considérés ici (la rotation d’ordre 5 peut être observée dans une structure non périodique, comme celles des quasi-cristaux).
Toutes ces opérations ne sont pas compatibles entre elles, (par exemple, on ne peut pas avoir à la fois un axe d’ordre 4 et un axe d’ordre 6 parallèles), et l'association de certaines provoquent l'apparition d'une nouvelle opération de symétrie (si on a un axe d’ordre 2 et un centre d'inversion, on a nécessairement un miroir). On recense ainsi 32 groupes ponctuels, qui sont toutes les combinaisons possibles des opérations citées ci-dessus, allant du groupe 1 qui ne contient aucune symétrie, au groupe m-3m, qui est le groupe le plus symétrique, celui du cube. Chaque groupe ponctuel est associé à un système cristallin.
Dans une maille multiple, deux autres opérations de symétrie font leur apparition :
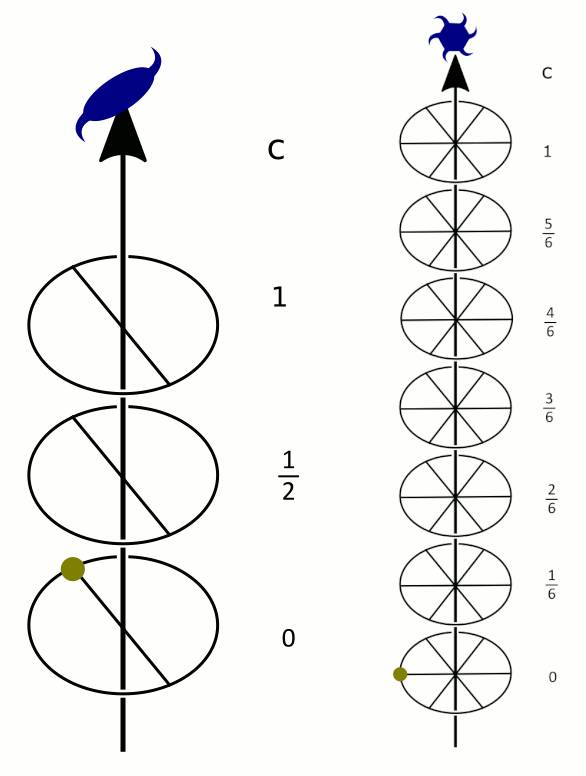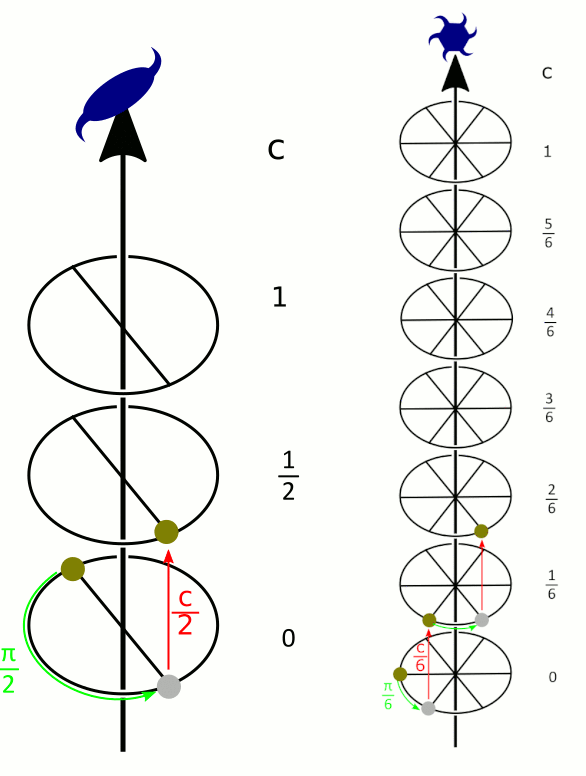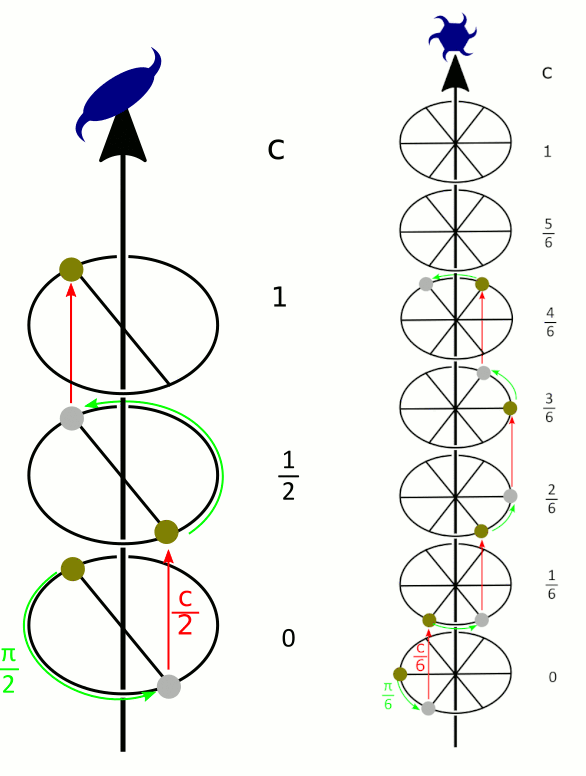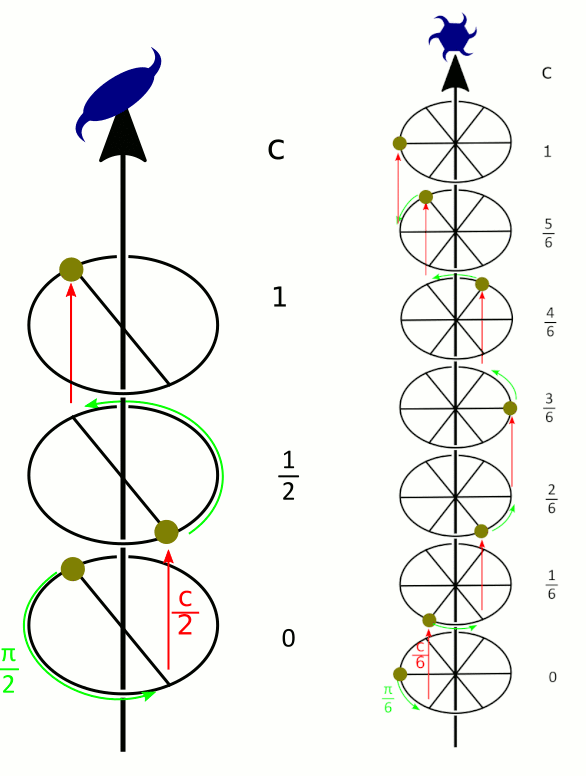
- les rotations translatoires, selon un axe dit hélicoïdal (Figure 9), qui sont la composée d'une rotation et d'une translation parallèle à l'axe de rotation. Elles sont notées nx : rotation d’ordre n et translation de x/n de maille.
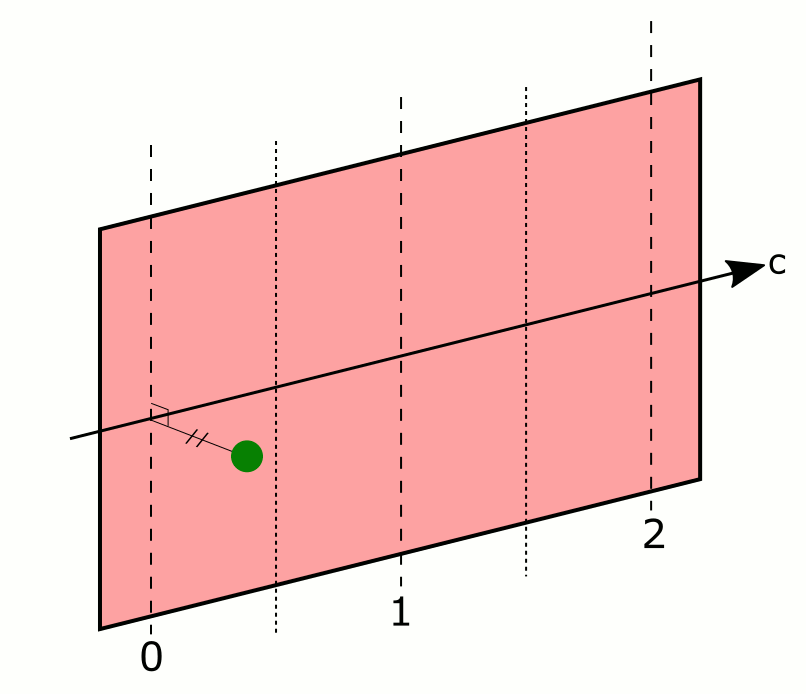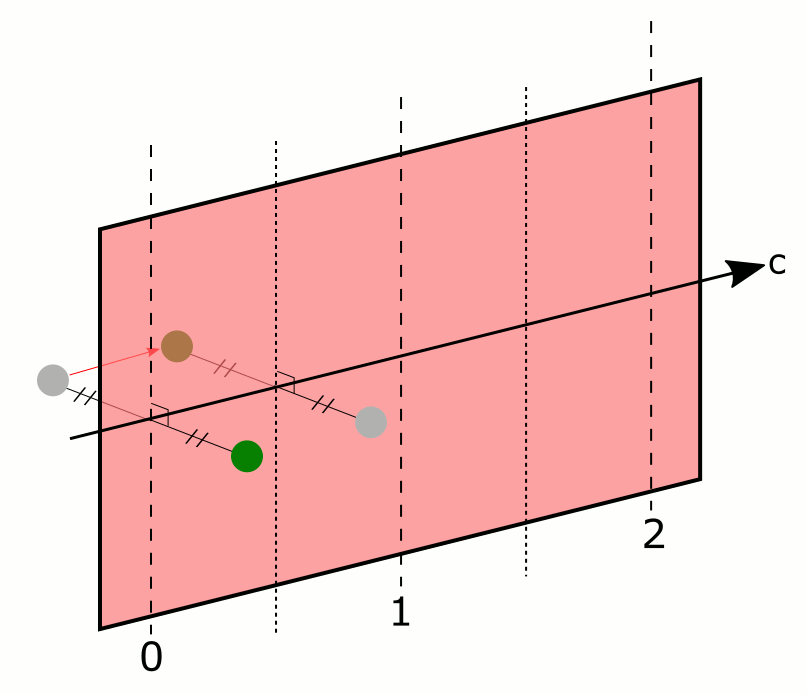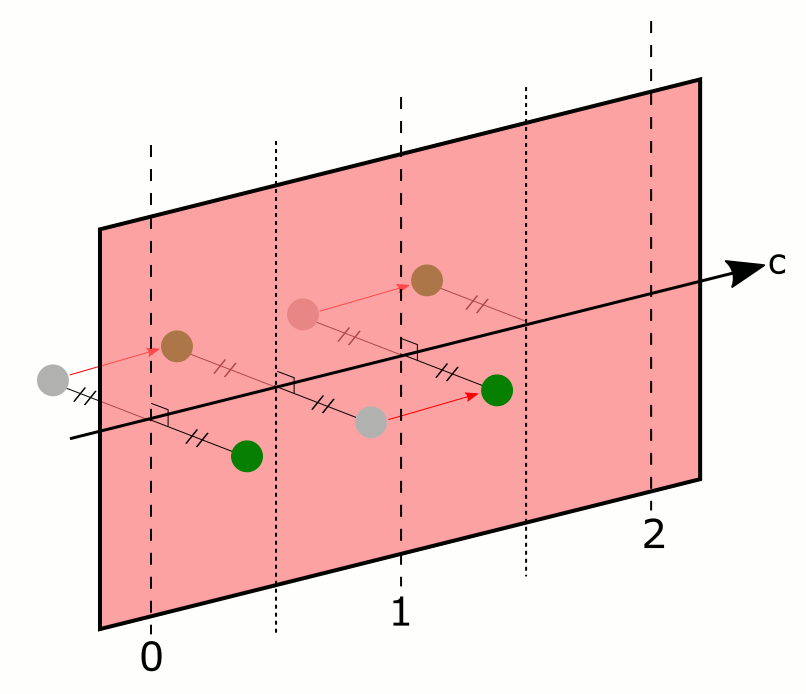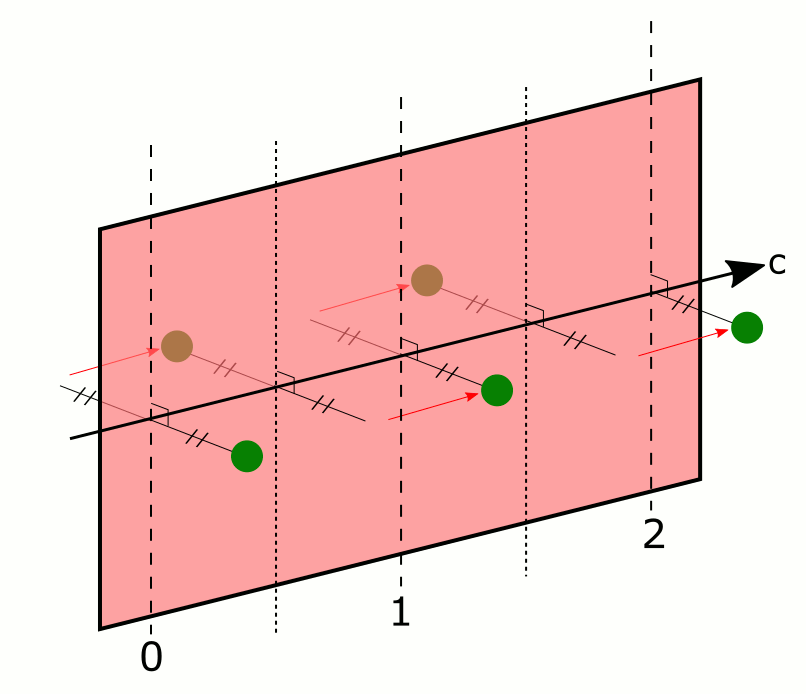
- les plans de glissement (Figure 10), qui sont la composée d’une réflexion et d'une translation parallèle au plan du miroir
À gauche, un axe 21 (rotation d'ordre 2, translation d'une demi-maille), à droite, un axe 61 (rotation d'ordre 6, translation d'un sixième de maille).
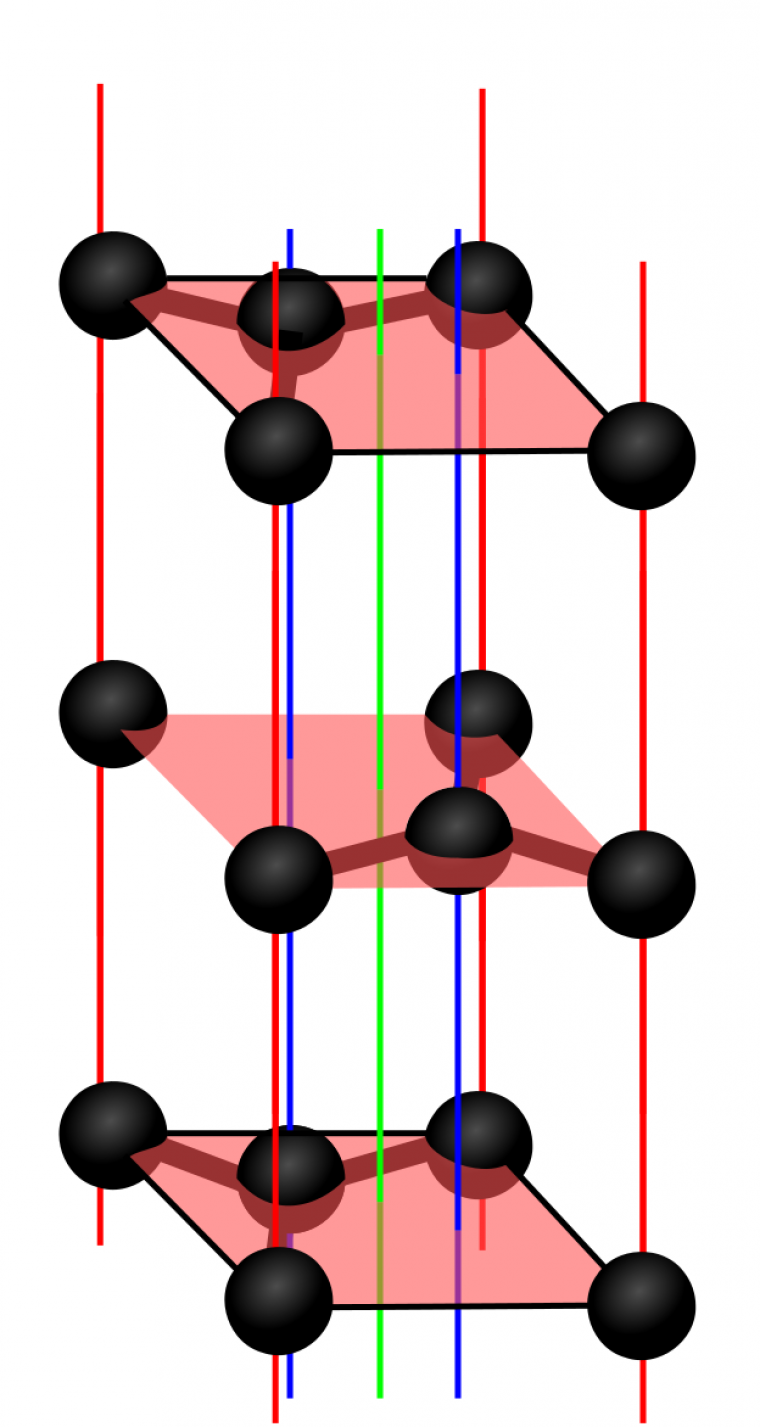
On retrouve l'exemple du graphite Figure 11.
En rouge, les axes 63 (rotation d'ordre 6, translation d'une demi-maille), en vert, l'axe 21 et en bleu les axes -6 (les centres d’inversion sont situés en z = 1/4c et z = 3/4c et sont repérés par des croix noires sur le schéma).
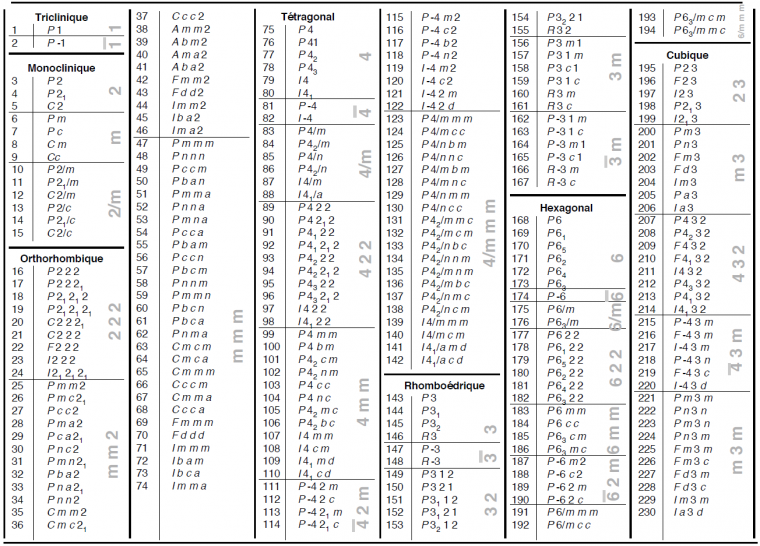
En rajoutant les opérations de symétrie translatoire, le nombre de groupes de symétrie, désormais appelés groupes d'espace, est de 230 (Figure 12). Chaque groupe d’espace est associé à un réseau de Bravais et est une variante d’un groupe ponctuel. Dans la nature, les groupes d'espace ne sont pas équiprobables. Une dizaine d'entre eux se partagent 50% des structures connues, alors que certains n'ont même jamais été observés.
Notons que chaque groupe d’espace est nommé selon son mode de réseau et les symétries portées par les axes d’intérêt.
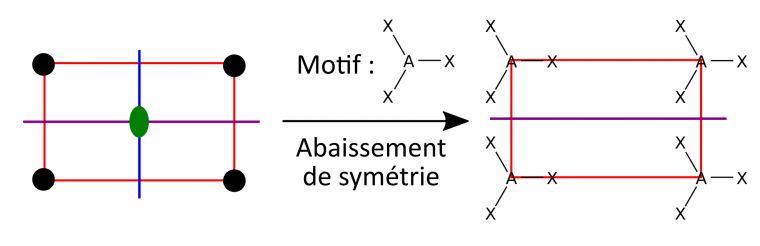
Intéressons-nous maintenant au cristal. Une fois que l'on remet le motif sur les nœuds du réseau, certaines opérations de symétrie peuvent disparaître. Le groupe d’espace de la structure du cristal peut donc être différent du groupe d’espace du réseau (qui, dépourvu d’atomes, est purement mathématique).
Quant au groupe ponctuel de la structure, il est souvent un sous-groupe du groupe ponctuel du réseau. Il est au mieux le même, notamment si le motif est un atome seul, comme dans le cas du fer pur, qui est cubique centré dans les conditions usuelles.
Exemple Figure 13:
Ici, on perd le miroir bleu et l'axe d'ordre 2 (ellipse verte, axe perpendiculaire à l'image) et on ne conserve que le miroir violet.
Bibliographie (commune aux quatre articles du dossier)
- Cours de cristallographie Livre III Première Partie Radiocristallographie Théorique, R. Gay, Gauthier-Villars et Cie, 1961
- Symétrie et Structure, J. Angenault, Vuibert, 2001
- Propriétés physiques des cristaux, leur représentation par des tenseurs et des matrices, J.F. Nye, Dunod, Paris, 1961.