Présentation

 

Dan Shechtman lors d'une conférence de presse en 2011.
Auteur(s)/Autrice(s) : Holger Motzkau, Wikipedia/Wikimedia Commons Licence : CC-BY-SA

La configuration obtenue par Dan Shechtman, un matin d'avril 1982, à partir d'un alliage aluminium-manganèse, était considérée comme impossible. Une bataille féroce s'engagea alors contre la science établie afin de faire valoir cette découverte. Le Prix Nobel de Chimie 2011 a fondamentalement modifié la façon dont les chimistes conçoivent la matière solide.

La découverte

C'est donc au matin du 8 avril 1982, qu'une image « contre-nature » fait son apparition dans le microscope électronique de Dan Shechtman (Figure 1). Jusqu'alors, au sein de la matière solide, il est admis que les constituants d'un cristal s'assemblent selon un motif symétrique se répétant périodiquement à l'infini. Cette répétition était la condition nécessaire à l'obtention d'un cristal.

Pourtant, l'image de Dan Shechtman montre que les atomes de son cristal s'assemblent selon un motif qui ne se répète pas !

Figure de diffraction obtenue par Dan Shechtman.

Un tel pavage était considéré comme impossible ; du même ordre que créer un ballon de football en utilisant uniquement des hexagones. Appréhender et imaginer un tel assemblage atomique est déjà une difficulté en soi dont la réponse sera apportée par l'art et les mathématiques.

 

Les mosaïques et les quasi-cristaux

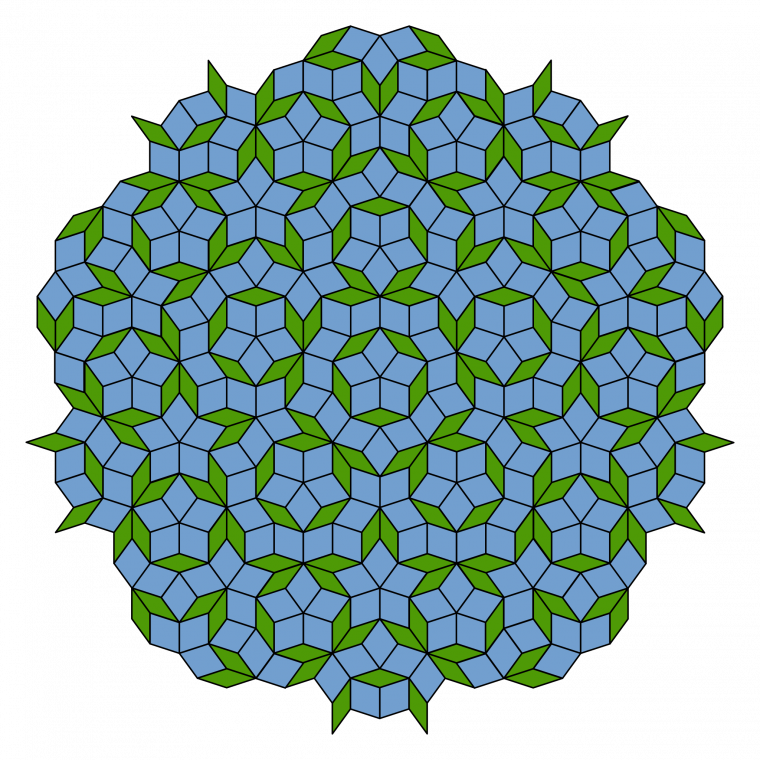
Depuis les années 1960, les mathématiciens s'intéressent à paver le plan à l'aide de motifs qui ne se répètent jamais afin de créer une mosaïque non-périodique. Au milieu des années 1970, Roger Penrose propose une solution élégante à ce problème : la pavage de Penrose (Figure 3).

Pavage de Penrose.
Licence : Domaine public

Les mosaïques non-périodiques de l'art islamique (comme celle du palais de l'Alhambra en Espagne ou du temple de Darb-i Imam en Iran) ont également aidé les scientifiques à la compréhension de la structure atomique d'un quasi-cristal (Figure 4). Dans ces mosaïques, comme dans les quasi-cristaux, les motifs sont réguliers - ils suivent une règle mathématique - mais ne se répètent jamais.

Exemple de mosaïque non périodique.

Quand les scientifiques décrivent les quasi-cristaux de Shechtman, ils utilisent le concept du nombre d'or, provenant de l'art et des mathématiques. Ce nombre apparaît souvent en géométrie et en architecture (notamment au niveau des temples de la Grèce Antique). Dans les quasi-cristaux, par exemple, le rapport entre les différentes distances inter atomiques est lié à ce nombre d'or.

 

Les quasi-cristaux : une curiosité de laboratoire ?

A la suite des découvertes de Shechtman, les scientifiques ont produit d'autres sortes de quasi-cristaux au sein des laboratoires. Mais ils ont également découvert des quasi-cristaux naturels dans des échantillons de minerais provenant de la rivière Khatyrka à l'est de la Russie.

Par ailleurs, une compagnie suédoise a trouvé des quasi-cristaux dans une forme particulière de l'acier, où les cristaux renforce le matériau telle une armure. Cet acier est actuellement utilisé dans des produits comme les lames de rasoir ou les aiguilles ultra-fines conçue spécifiquement pour la chirurgie de l'oeil.

Du fait de cette faculté à renforcer les matériaux, les scientifiques expérimentent également l'utilisation des quasi-cristaux au sein de machines soumises à de hautes températures et/ou pression comme les moteurs Diesel.

 

Bibliographie et Ressources en Ligne

  1. Shechtman, D., Blech, I., Gratias, D., and Cahn, J.W. (1984) Metallic phase with long-range orientational order and no translational symmetry, Phys. Rev. Lett. 53(20):1951-1954.
  2. Conférence de Denis Gratias, chercheur émérite au CNRS, sur les quasi-cristaux, diffusée sur Canal-U.
  3. Pour compléter cet article, vous pouvez consulter le site concernant le Prix Nobel de Chimie 2011 et en particulier les ressources données par l'Académie Royale des Sciences de Suède.